salut

Bonjour
Nous avons max(f(x,y))= -min(-f(x,y))
Donc min(-2x+y+4)=4-max(2x-y)
On peut appliquer le faite que:

Donc min(-2x+y+4)=4-max(2x-y)=

Ou bien min(x,y)=4-max(2x-y)
C'est difficile d'utiliser simplexe dans ce cas
Merci beaucoup

Bonjour
Une indication s'il vous plaît
Merci beaucoup d'avance

je ne vois absolument pas en quoi ce 4 te gène ...

puisque min (a + 4) = (min a) + 4

Nous avons
Min (z)=min(x₁,x₂)=min(-2x₁+x₂)+4
Ce 4 me gêne beaucoup
Ou bien je fait la méthode de simplexe sans +4 et je l'ajoute aux résultats finale de solution optimale je ne comprends pas comment faire
Merci beaucoup

Salut,
Je serais tenté de remplacer les >= par des <=

Bonjour
J'utilise donc la méthode de dualité mais le +4 sera toujours présent je voulais l'éliminer pour utiliser la méthode simplexe normalement .

M-4=-2x1+x2
Tu cherches le minimum de M-4 par l'algorithme
Tu en déduis le minimum de M

Bonjour
D'accord, nous avons :
Forme standard correspondante:




Merci beaucoup

Quelle est ta reponse ?

Bonjour

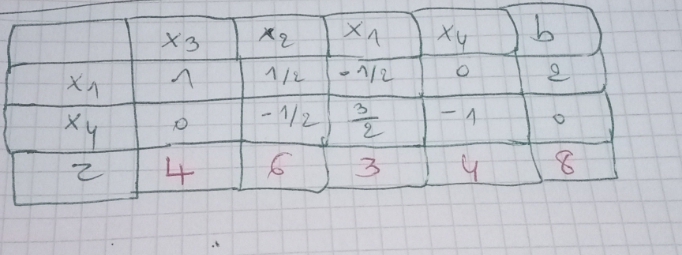
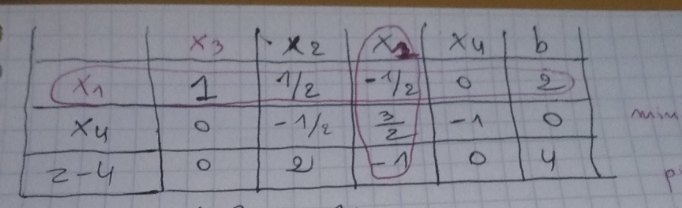
Puisque les valeurs de z sont positifs donc la valeur optimale est z*=8
Les variables de bases sont:
(x₁*,x₄)=(2,0)
Merci beaucoup

Peux tu relire l'énoncé du premier post et le confirmer

Bonjour
Je confirme ma réponse
Merci beaucoup

Que se passe t il si x1 tend vers plus l'infini et x2=0 ?

Bonsoir
Comment je calcule la limite je ne comprends pas
Merci beaucoup

En reprenant l'énoncé initial
Si x1=1000 et x2=0 que vaut z ?

Bonjour
z=-1996 mais pourquoi ma méthode de simplexe n'est pas bonne
Merci beaucoup

Je ne sais pas, le mieux est de demander une relecture de l'énoncé à la personne qui te l'a proposé.

Bonsoir à tous,
C'était notre prof qui nous la proposé
Merci beaucoup

Bonjour à tous
S'il vous plaît il y a quelqu'un qui aura une idée pour ce problème merci beaucoup d'avance

Bonjour,

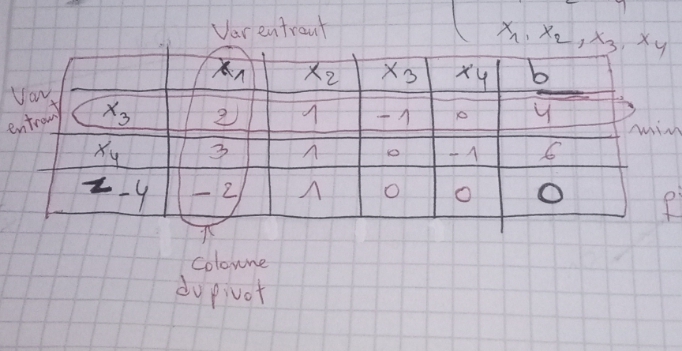
cela fait longtemps que je n'ai pas fait de simplex, mais j'aurai démarré par :
x1 x2 x3 x4 b
x3 2 3 -1 0 4
x4 3 1 0 -1 6
z -2 1 0 0 4

cette matrice n'est pas canonique à cause des -1 qui apparaissent à cause de x3 et x4.  Dans ce genre de cas, je croix  qu'on
introduit 2  variables artificielles x5 et x6 .

x1 x2 x3 x4 x5 x6 b
x3 2 3 -1 0 1 0 4
x4 3 1 0 -1 0 1 6
z -2 1 0 0 1 1 4

vérifiez dans votre cours.