Bonjour

j'ai une petite difficulté à résoudre cet exercice

De façon à protéger son entreprise contre une éventuelle pollution du littoral qui conduirait à l'interdiction de la vente des coquillages récoltés, monsieur Ixe souhaite diversifier son activité. Il envisage ainsi la préparation et la vente de semi- conserves (marinades, soupes, lasagnes de fruits de mer, … ) aux particulier et aux  supermarchés.

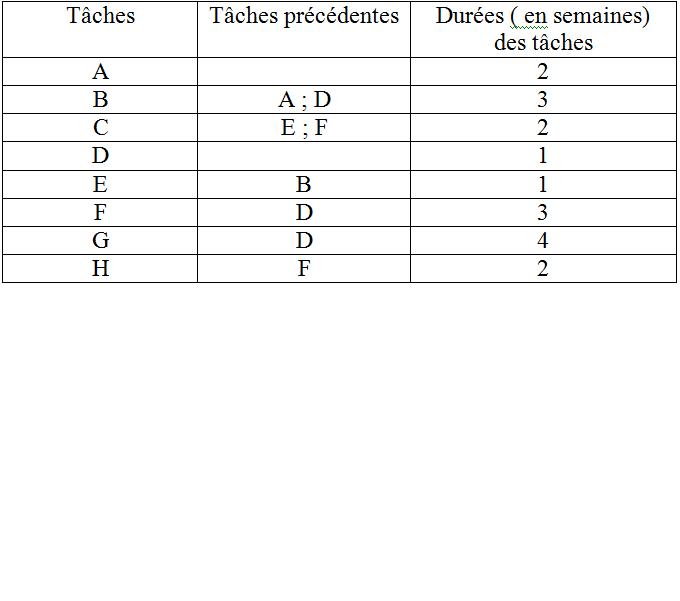
Les différentes tâches nécessaires à la mise en place de cette nouvelle activité, leurs durées (exprimées en semaines) et les contraintes d'antériorités qui doivent être respectées entre les tâches, sont répertoriées dans le tableau ci- dessous :

Tâches Tâches précédentes Durées ( en semaines) des tâches
A 2
B A ; D 3
C E ; F 2
D 1
E B 1
F D 3
G D 4
H F 2

1°- Construire le graphe MPM formalisant le projet.  ok
2°- Quelles sont les tâches critiques ? Dans combien de temps, au plus tôt monsieur Ixe pourra-t-il débuter sa nouvelle activité ? ok (8 semaines)
3°- Calculer les marges totales et les marges libres des différentes tâches.ok
4°- la durée (exprimée en semaine) de la tâche H est,  en réalité, une variable aléatoire. On admet qu'elle suit une  loi exponentielle : P ( x ) = 0,5 exp ( - 0.5 x ).
a- Quelle est la probabilité que la date de début  de la nouvelle activité soit retardée ?
b- Vérifier que la durée de 2 semaines de la tâche H, indiquée sur le tableau, correspond à la durée moyenne de cette tâche.
La définition de la fonction de répartition de la loi exponentielle est :
F(x) = p( X≤ x ) = 1 - exp(-0,5 x ) ; pour toutes valeurs de x

mon souci est au niveau de la 4 question

Merci d'avance pour vos indications et réponses