Inscription / Connexion Nouveau Sujet
Minimum d'une fonction, sans formule
Bonjour à tous 
(pardon pour la notation calculatrice moche avec les sqrt, je suis pas capable de faire des signes racine carrée)
Je suis bloqué sur cet exercice.
"Où placer le pont [KH], perpendiculaire aux berges de la rivière, supposées parallèles, pour que la longueur du trajet de A à B soit la plus petite possible ?"
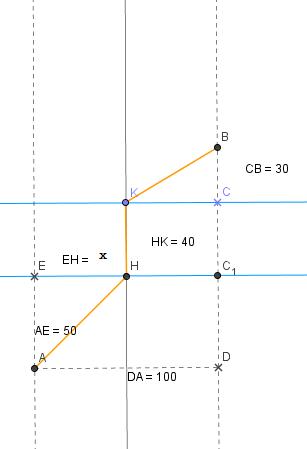
Le trajet est en orange, les points représentés par une croix sont ceux qui ne sont pas directement dans l'énoncé mais que j'ai utilisé.
J'ai défini f(x) comme AH + HK + KB (dans l'intervalle [0;100])
AH= sqrt(50² +x²) = sqrt(x² +2500)
KH= 40
KB= sqrt(30² +(100-x)²) = sqrt(x² -200x + 10900)
d'où f(x)= sqrt(2x² -200x + 15000)
(j'ai pu me tromper rien que là...)
Ca donne bien une parabole, le minimum c'est bien le sommet de cette parabole, ça fait x=50, mais...
- La détermination graphique est un peu "light"
- Je n'ai pas vu les dérivées
- Je n'ai pas non plus le droit aux formules des fonctions ax²+bx+c, puisqu'on les a pas vues non plus.
Comment dois-je déterminer ce fichu minimum ? Je vais m'en arracher les cheveux 
D'avance merci à ceux qui prendront la peine de friser la calvitie avec moi 
Edit Coll : image placée sur le serveur de l'  Merci d'en faire autant la prochaine fois !
Merci d'en faire autant la prochaine fois ! 
![]()
Tu n'as aucune précision de la manière dont tu dois déterminer ce minimum ? Est ce que tu es sur que la détermination graphique n'est pas autorisée ?
Sinon, une autre question, dans quel chapitre de maths es-tu en ce moment ? Ça pourrait te donner une piste de réflexion.
Ce sont les fameux exercices en fin de chapitre, "prendre des initiatives", "pour aller plus loin" en fin de chapitre...  (après aucun exercice d'entrainement, mais ça...)
(après aucun exercice d'entrainement, mais ça...)
Je n'ai aucune précision mais je trouve qu'une simple détermination graphique est un peu simple pour un exercice du genre, ça ne fait rien "chercher".
Le chapitre est sur les variations des fonctions (avec l'histoire de l'ordre qui change ou qui ne change pas). Je pourrais chercher quand la fonction cesse d'être décroissante sur l'intervalle [0;100], mais c'est du "à tâtons"...
Je suis arrivé à f(100-x) = f(x), je pense pouvoir faire quelque chose avec ça, mais je ne vois pas trop quoi, je n'arrive pas à visualiser ce que ça peut bien représenter... (si ça se trouve c'est complètement inutile)
Je suis dans la meme situation que toi, aujourd'hui.. J'ai retourné le probléme dans tout le sens, et 'est à la veille de le rendre, que j'ai pensé à e forum.. POurrais-tu m'aider, m'expliquer ta démarche pour réussir ? merci beaucoup !!
Bonsoir
J ai un dm avec le même schéma mais pas les même questions
On cherche ou placer le pont [AB] , perpendiculaire aux berges de la rivière,
supposees parallèles, pour que la longueur du trajet de O a M soit la plus petite possible. On pose
X= EH et on note xo la valeur de x pour laquelle L = AH +HK+KB
1) on considéré la fonction f définie sur [0,100] par f(x) = AH+HK+KB
Montrer que f(x) = √50 au carre +√ x au carre + 40 + √30 au carrre + (100-x) au carre
J ai fait pythagore dans AEH
AH au carre = AE au carre + EH au carre
AH au carre = 50au carre + x au carre
AH = 2500+x
Et après j ai fait pytagore dans KBC
KB = x au carre-200x+10900
C est ça que je dois faire?
Ce suffit a démontrer ou pas
Merci d avance pour votre aide
Bonjour,
Quelque un pourrait me dire si mon raisonnement est bon ? Je dois bien faire pythagore? Si c est bon?
Merci d avance
bonjour,
le raisonement est bon mais les calculs complètement faux.
AH2 = AE2 + EH2 OK (il y a un bouton X2 pour mettre des exposants)
AH2 = 502 + x2 OK
AH = 2500+x n'importe quoi !!
AH =  (2500 + x2) et ça ne se simplifie pas !
(2500 + x2) et ça ne se simplifie pas !
tu fais pareil de l'autre côté du pont pour BK
et tu dois obtenir
AH + HK + BK =  (2500 + x2) + 40 +
(2500 + x2) + 40 +  (.....)
(.....)
c'est à dire
et on ne peut pas jongler avec ce qu'il y a sous les radicaux comme ça pour le "simplifier" !!
ta recopie de l'énoncé est complètement fausse !!
f(x) = √50 au carre +√ x au carre + 40 + √30 au carrre + (100-x) au carre
faux ! tu as écrit :
etc qui est totalement FAUX
et différent de ce qui est réellement marqué sur ton énoncé :
qui traduit "en ligne" serait
f(x) = √502 + x2
+ 40 + √
302 + (100-x)2
Ok merci pour tes explications je vais faire plus attention pour écrire un texte pour la prochaine fois et peux tu m expliquer comment on fait les grandes racines .
Pour BK c' est racine de 900 + (100-x)[sup][/sup]?
J ai appuyé sur la touche x2 j espère que c était comme ça
Merci d avance pour ta réponse
Tu peux aussi vérifier ton message avec la touche "Aperçu".
la touche X2 est du même usage que dans les traitements de texte : elle "passe en mode exposant" c'est à toi de taper la valeur de cet exposant (ici 2), ou bien elle "met en exposant" le texte sélectionné : un texteexposant
pour les grandes racines :
- soit les symboles spéciaux avec la palette appelée par le bouton  , on y trouve le symbole
, on y trouve le symbole  , mais c'est à utiliser sous la forme
, mais c'est à utiliser sous la forme  ( bla bla ) praenthèses pour préciser ce qui est "sous la racine" sinon c'est le terme juste qui suit et seulement lui. (priorité des opérateurs !!)
( bla bla ) praenthèses pour préciser ce qui est "sous la racine" sinon c'est le terme juste qui suit et seulement lui. (priorité des opérateurs !!)
- soit carrément en LaTeX. Mode d'emploi succinct ![]() [lien] (lien
[lien] (lien  en haut de la page)
en haut de la page)
Ceci dit, retour au problème lui-même. tu trouves bien (en corrigeant l'exposant)
BK c' est racine de 900 + (100-x)2?
BK =
 (302 + (100-x)2) (parenthèses pour bien préciser la portée de "racine") OK.
(302 + (100-x)2) (parenthèses pour bien préciser la portée de "racine") OK.
Cela se voit d'ailleurs dans l'énoncé puisqu'il donne le résultat attendu :
"montrer que ... = formule", il suffit de comparer avec la formule donnée dans l'énoncé !!


