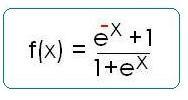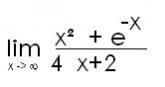
bonjour

a) arg(z²)=2arg(z) (2Pi)
arg(-iz)=3Pi/2+arg(z) (2Pi)
donc
arg(z²)=arg(-iz) ssi 2arg(z)=3Pi/2+arg(z)+2kPi   ; k entier relatif
                 ssi arg(z)=3pi/2 +2kPi
                 ssi z=-iy et y>0
                 ssi M appartient demie-doite Oy privée de O et dirigée vers les y négatifs

b) en+oo e^-x tend vers 0+ donc lim(x²+e^-x)/(4x+2)=lim(x/4)=+oo
en -oo e^-x tend vers +oo
f(x)=(4x+e^-x/x)/(4+(2/x))
    =(4x-(e-x/-x))/(4+(2/x))
2/x tend vers 0
e^-x/-x tend vers +oo lorsque x tend vers -oo
donc limf(x)=-oo en -oo

c) f(x) illisible

c)

Merci pour les réponses précédentes


(désolé pour le c)

c)Etudier les variations de la fonction f définie sur R par

c) f(x)=1 c'est une constante

Ha d'accord. Merci watik pour ton aide C'est gentil d'avoir pris le temps de répondre.

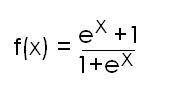
Bonsoir,

Je me permet de poster un exercice et j'aurai besoin d'une correction. Merci à ceux qui voudront bien me répondre

Exercice: déterminer (img)

Réponse : Lim (x²/4) =  lim x² (numérateur du plus haut degré) = + oo
          Lim (e^-x / 2+x) = lim e^-x = 0
          Donc par addition, la limite tend vers + oo



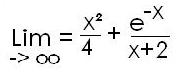
*** message déplacé ***

c'est bon.

*** message déplacé ***

Bonsoir

C'est correct

*** message déplacé ***

Ha merci beaucoup pgeod & yogodo. Bonne soirée!


*** message déplacé ***

*** message déplacé ***

Bonsoir,

et si on avait