Inscription / Connexion Nouveau Sujet
Morphisme de groupes
Bonjour,
Il y a des choses qui me posent questions concernant les morphismes de groupes, et je voudrais savoir si ce qui est mis ci-dessous est juste.
1°)- Même si un morphisme ne se résume pas qu'à cela, si un morphisme est bien une application qui va d'un ensemble à un autre, un morphisme de groupes est bien un application qui va d'un groupe à un autre.
2°)- Si est un morphisme de groupes, c'est obligatoirement une application, donc tout élément de son ensemble de départ a une image et une seule dans son ensemble d'arrivée,
comme par exemple :
De ce fait, l'ensemble de départ (muni de la LCI qu'on lui attribue) d'un morphisme de groupes doit donc obligatoirement correspondre au domaine de définition (ensemble muni de la LCI qu'on lui attribue) de la fonction considérée.
Vous remerciant.
Bonjour.
Oui à tout.
Un morphisme de groupes, c'est avant tout une application, d'un groupe dans un autre, avec ce que ça implique (unicité de l'image, etc.).
Pour essayer d'aller plus loin, je dirais.
Mettons que l'on a une fonction :
On "réduit" cette fonction à une application :
Est-il possible alors d'avoir un morphisme de groupe
avec :
et
Vous remerciant.
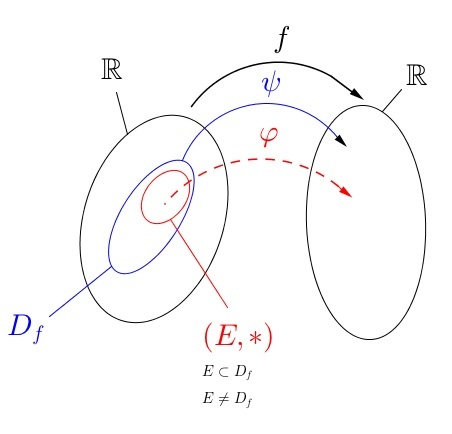
Si un tel E existe alors oui, il suffit de prendre l'identité.
Juste par curiosité, pourquoi te poses-tu cette question ? Son intérêt ne me saute pas aux yeux.
Merci beaucoup de tes réponses.
Je comprends que l'intérêt ne te saute pas aux yeux.
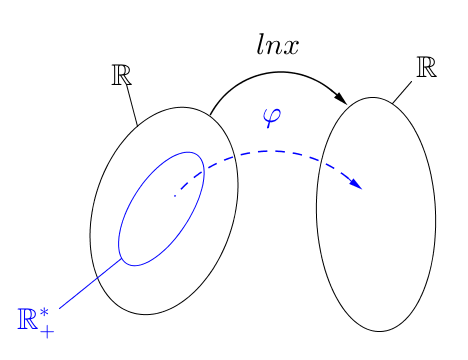
En fait, au début j'étais parti là-dessus (voir figure), mais ça ne marche pas avec .
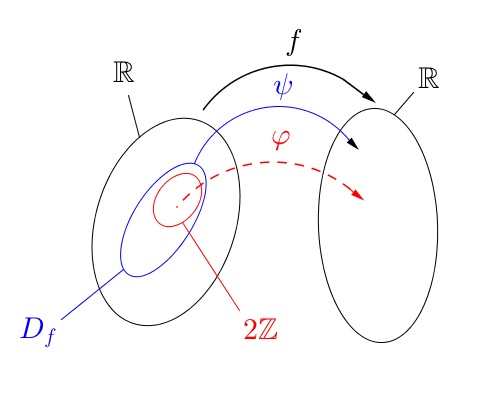
Après je me suis dit prenons , mais là on ne peut avoir un morphisme de groupe car
ne peut être un groupe.
Donc c'est là que sont venues poindre les questions posées dans le présent topic.
Mais peut-être (sûrement) que je ne me pose pas les questions dans le bon ordre, et que maintes de mes questions trouveront réponse dans la progression de l'apprentissage de mon cours.
Bonjour
Je ne comprends pas trop ce qui"ne marche pas" avec ln ?
Son ensemble de définition est R+* dans lequel la multiplication est interne, et à qui cette même multiplication confère une structure de groupe. Son ensemble d'arrivée est R qui, muni de l' addition, est aussi un groupe. Et ln est bien un homomorphisme entre ces deux groupes, non ?



 algèbre en post-bac
algèbre en post-bac