Inscription / Connexion Nouveau Sujet
Desole j'ai repondu a cote.
Tu as OH*OM = OA*OB
or OM =(a+b)/2 et OA= a et OB=b donc OH = ab/[(a+b)/2] = 2ab/(a+b)
qui est bien la valeur demandee
*** message déplacé ***
Moyenne harmonique (2)
Salut à tous,
Je suppose que le topic a été fermé car 1 topic = 1 problème.
Je re-poste donc mon nouveau problème dans un nouveau topic.
![]() Moyenne harmonique.
Moyenne harmonique.
Moyenne harmonique :
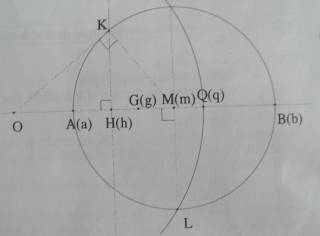
Le point cherché est la projection orthogonale du point K sur la droite (AB). Exprimer cos KÔH en fonction des longueurs des côtés dans le triangle OHK rectangle en H. Exprimer sin KMO en fonction des longueurs des côtés dans le triangle OKM rectangle en K.Justifier que cos KÔH = sin KMO. Déduire de cette égalité que OK² = OH * OM. Remplacer OK et OM par les valeurs précédemment obtenues et conclure. Montrer que le point H du segment [AB] vérifie aussi la condition OA/OB = HA/HB (transformer l'égalité en utilisant les abscisses des points et retrouver h = 2ab/(a+b) ).
cos KOH = OH/OK
sin KMO = OK/OM
Dans OKM rectangle en K : KOH et KMO sont complémentaires donc le sinus de l'un est égal au cosinus de l'autre. Ce qui revient à OH/OK = OK/OM d'où OK² = OH * OM.
Je suppose que les valeurs précédemment obtenues sont celles trouvées par Minkus soit OK² = OA x OB.
Ainsi, OK² = OH x OM = OA x OB.
Donc OK = g = V(ab)
Montrer que le point H du segment [AB] vérifie aussi la condition OA/OB = HA/HB (transformer l'égalité en utilisant les abscisses des points et retrouver h = 2ab/(a+b) ).
Je ne sais pas comment faire cette dernière question.
Je tiens à remercier Minkus et Youpi et bien sur et surtout Philoux pour leur grande aide et leur patience.
Je tiens à m'excuser auprès des modos, j'aurais dû créer plusieurs topics différents sachant que 1 topic = 1 problème.
J'ai aussi créé un nouveau topic, les grands esprits se rencontrent... non je rigole je suis loin d'être un grand esprit !
Merci de ta réponse.
--------------
Estelle.
*** message déplacé ***
STL,
ton topic a été fermé automatiquement parce qu'il a atteint les 100 messages ! Ce qui est déjà énorme pour la résolution d'un problème 
okay
thales je ne vois pas dans quels triangles,
en revanche avec la meme methode que l'autre et le cosinus de l'angle KMH tu peux montrer que MH/MK = MK/MO
et travailler avec ca ensuite
Ah ok Océane.
Il faut dire que c'est un problème assez long et c'est surtout que Philoux a du détailler et ré-expliquer beaucoup de choses que je n'avais pas comprises.
dans KMH rect. en H : cos KMH = MH/MK
dans OKM rect. en K : cos KMO = MK/MO
Donc MH/MK = MK/MO, soit MK² = MH x MO
Je suis desole mais je n'ai plus le temps de chercher.
Bon courage, je pense que tu peux faire la suite en passant cette question.
En effet si OA/OB = HA/HB
alors a/b = (h-a)/(b-h) et avec le produit en croix tu retrouves facilement la valeur demandee
Je suis desole mais je n'ai plus le temps de chercher.
Bon courage, je pense que tu peux faire la suite en passant cette question.
En effet si OA/OB = HA/HB
alors a/b = (h-a)/(b-h) et avec le produit en croix tu retrouves facilement la valeur demandee
ce que tu as fait a 20h16 est bon et n'oublie pas que MK = MA = MB
avec ca (et peut-etre aussi avec OH*OM=OA*OB mais ca m'etonnerait) tu peux peut-etre arriver a OA/OB = HA/HB mais ca l'air d'etre des gros calculs et la tout de suite je ne le vois pas
ce que tu as fait a 20h16 est bon et n'oublie pas que MK = MA = MB
avec ca (et peut-etre aussi avec OH*OM=OA*OB mais ca m'etonnerait) tu peux peut-etre arriver a OA/OB = HA/HB mais ca l'air d'etre des gros calculs et la tout de suite je ne le vois pas
Merci beaucoup. A demain.
Merci à minkus d'avoir pris le relais (ainsi qu'à Youpi  )
)
Ton problème est peut être long mais il est très intéressant : il permet d'appréhender un peu mieux toutes ces moyennes.
Il mériterait de faire l'objet d'un exo résolu sur l'île...
Philoux
Bonjour,
Tout a fait d'accord Philoux ce mélange d'algèbre et de géométrie est des plus plaisants, surtout à un niveau comme la seconde. L'année ou j'ai enseigné en 2nde j'ai proposé le meme exercice sur les moyennes mais de facon bcp plus simple car on n'utilisait que le théoreme de Pythagore. Le but était de comparer toutes ces moyennes qui sont toujours rangées dans le meme ordre quadratique > arithmetique > geometrique > harmonique (si mes souvenirs sont bons). On pouvait les comparer par des considérations géométriques assez simples (l'hypoténuse des triangles rectangles étant tjs le plus grand coté). Ensuite on retrouvait le résultat par des démonstrations algébriques qui permettaient de voir les différentes méthodes de comparaison de nombres : en comparant les carrés, en étudiant le signe de la différence etc...
Si je remets la main sur ce "vieux truc", je te fais signe Estelle 
bonjour minkus
On peut même ajouter, en prenant le cas de 2 valeurs a<b :
a < Mharmonique(a,b) < Mgeometrique(a,b) < Marithmetique(a,b) < Mquadratique(a,b) < b
dans le cas de n valeurs, a_i, de a_1 à a_n, est-ce que le "a" c'est le min et "b" le max de ces valeurs ?
Philoux
Philoux
Bonjour à tous les deux,
il y a bien une conclusion à cet exercice :
Ordre entre les différentes moyennes :
La figure précédente permet d'observer géométriquement que les diffémentes moyennes sont rangées dans l'ordre :
a < h < g < m < q < b soit encore a < 2ab/(a+b) < V(ab) < (a+b)/2 < (V2)/2xV(a²+b²) < b.
Démontrer cs inégalités.
Penser à utilier si A > 0 et B > 0 alors A < B équivaut à A² < B².
Si je remets la main sur ce "vieux truc", je te fais signe Estelle
Merci Minkus.
Je vais bientot m'y mettre d'ailleurs mais il me reste avant application et l'interprétation géométrique de la moyenne quadratique, à savoir :
Interprétation :
Justifier que la longueur de la diagonale du rectangle de côté a et b est égale à la longueur de la diagonale du carré de côté q.
J'ai écrit :
soit un rectangle de côté a et b, d = V(a²+b²)
soit un carré de côté q , d = V(2q²)
On veut montrer que V(a²+b²) = V(2q²)
Sachant que q = (V2)/2 x V(a²+b²)
Application :
L est le point d'intersection du cercle de centre M passant par A et B. Q est le point du segment [AB] tel que OL = OQ. En utilisant le triangle OML rectangle en M, montrer que l'on a bien OL = V2/2 x V(a²+b²).
Si les diagonales ont meme longueur alors leurs carres aussi donc oublie les racines.
d^2 = a^2 + b^2 et d'^2 = q^2 + q^2 =2q^2
or on a evidemment a^2 + b^2 = 2q^2 avec la definition de q (en mettant au carre)
pour OL fais Pythagore et n'oublie pas que ML = MA = AB/2 et que OM = (a+b)/2
Merci à minkus d'avoir pris le relais (ainsi qu'à Youpi )
De rien j'ai vraiment pas été d'une grande aide sur ce coup là !

Bonjour,
merci minkus.
OM² + ML² = OL²
[(a+b)/2]² + (AB/2)² = OL²
d'où OL = V ( [(a+b)/2]² + (AB/2)² )
Je pense que j'ai fait une erreur quelque part parce que je trouve :
OL = V ( [(a+b)/2]² + (AB/2)² )
= V ( [(a+b)/2]² + [(b-a)/2]² )
= V [ (a²+2ab+b²)/4 + (b²-2ab+a²)/4 ]
= V(2a²+2b²)/2
= V(a²+b) or q = (V2)/2 x V(a²+b²)
salut estelle
le 2 sous la racine donne V2 : il ne se simplifie pas avec le 2 du dénominateur...
Philoux
Salut Philoux,
merci, je n'avais pas fait attention à ça.
J'ai donc :
= V [ (a²+2ab+b²)/4 + (b²-2ab+a²)/4 ]
= V [ (2a²+2b²)/4 ]
= V (2a²+2b²) / 2
= [ V2 x V(a²+b²) ] / 2
= (V2)/2 x V(a²+b²) or q = (V2)/2 x V(a²+b²) d'où OL = q.
C'est tout bon Estelle mais personnellement je connais une expression plus simple de q.
q =  [(a^2+b^2)/2]
[(a^2+b^2)/2]
Autrement dit la moyenne quadratique est la racine carree de la moyenne arithmetique des carres. 
Autrement dit la moyenne quadratique est la racine carree de la moyenne arithmetique des carres.
Merci Minkus  Je vais m'embrouiller avec toutes les moyennes, surtout si on établit des rapports entre elles !
Je vais m'embrouiller avec toutes les moyennes, surtout si on établit des rapports entre elles !
Tu sais quoi, quand ton prof te donnera ta moyenne du 2e trimestre tu lui diras que toi tu as trouve plus. Tu lui diras qu'il n'a pas precise qu'il s'agissait de la moyenne arithmetique et que toi tu as calcule avec la moyenne quadratique.
C'est garanti, la quadratique est tjs meilleure que l'arithmetique !
 :D
:D

je crois que je m'en souviendrais maintenant ! 
Mais je pense que je ne le ferai pas, ma prof est du genre "Puisque tu viens réclamer des points et que tu as tort (car j'ai toujours raison), je t'enlèverai 1 point sur ta moyenne du prochain trimestre..."
Un exemple : cette prof ne mettra jamais 20 à une copie même si sur le barême ce devrait être 20, car 20 c'est parffait, or la perfection n'existe pas. Et quand on a comme moi 19 au lieu de 20 juste parce que "la perfection n'existe pas", c'est vraiment rageant.
Ordre entre les différentes moyennes :
La figure précédente permet d'observer géométriquement que les diffémentes moyennes sont rangées dans l'ordre :
a < h < g < m < q < b soit encore a < 2ab/(a+b) < V(ab) < (a+b)/2 < (V2)/2xV(a²+b²) < b.
Démontrer cs inégalités.
Penser à utilier si A > 0 et B > 0 alors A < B équivaut à A² < B².
j'ai déjà démontré que :
a < 2ab/(a+b) < b
a < V(ab) < b
a < (a+b)/2 < b
a < (V2)/2xV(a²+b²) < b
donc il me reste à montrer que
2ab/(a+b) < V(ab) < (a+b)/2 < (V2)/2xV(a²+b²)
je ne sais pas comment faire pour démontrer une suite d'inégalités. Je suppose que je dois les démontrer deux à deux. C'est la bonne marche à suivre ? (que je ne me lance pas dans des calculs inutiles s'il y a plus simple ^^)
Oui c'est la bonne methode et tu as donc seulement 3 comparaisons a faire.
h < g puis g < m et enfin m < q
Comme a chaque fois il y a un nombre avec un radical on te conseille de passer au carre pour le faire degager.
Ensuite tu as besoin d'utiliser de facon astucieuse les identites remarquables mais sur ca je te fais confiance.
Voyons pour h < g :
2ab/(a+b) < V(ab)
(2ab/(a+b))² < ab
4a²b² / (a+b)² < ab
Je ne pense pas qu'il faille développer parce que sinon ce ne serai pas pratique pour simplifier la fraction. Ai-je raison/tort ?
Il y a une autre methode tres importante a connaitre : "pour comparer deux nombres, on peut etudier le signe de leur difference".
Mais tu peux aussi t'en sortir avec ton resultat.
Tu mulitplies tout par le denominateur et tu divises tout par ab.
4a²b² / (a+b)² < ab
4a²b² < ab (a+b)²
4ab < (a+b)²
Autre méthode :
il faut montrer que V(ab) - 2ab/(a+b) > 0
mais là je serais tenter d'en revenir à V(ab) > 2ab/(a+b)
donc je tourne en rond ! je ne suis pas habituée à comparer en étudiant le signe de la différence, bien que je sache que c'est possible..
Je dois y aller
"tu dois te coucher tôt Estelle car tu as cours demain" ^^
merci encore de ton aide Minkus et merci à philoux aussi pour son intervention
je posterai le résultat de mes "recherches" demain matin.
Bonsoir à tous.
Tu peux etudier le signe de la difference a n'importe quel moment et ici il fallait d'abord passer au carre.
D'ailleurs tu peux le faire aussi la ou tu es rendu.
Etudie le signe de (a+b)^2 - 4ab
Bonne nuit.
minkus
Bonjour,
4a²b² / (a+b)² < ab
4a²b² < ab (a+b)²
4ab < (a+b)²
Etudie le signe de (a+b)² - 4ab
= a² + 2ab + b² - 4ab
= a² + b² - 2ab
= (a-b)² or un carré est toujours positif donc (a+b)² - 4ab est positif.
Puisque (a+b)² - 4ab est positif alors 4ab < (a+b)².
bonjour Estelle (matinale ?)
4ab < (a+b)²
plus rapide
4ab < a²+2ab+b² <=> 0 < a²-2ab+b² <=> 0 < (a-b)² toujours vrai puisque a différent de b
Philoux
Salut Philoux (oui, matinale)
Comment passes-tu de 4 ab < a²+2ab+b² à 0 < a²-2ab+b² ?
En retranchant 4ab aux deux membres ?
en faisant passer le 4ab de gauche vers la droite (il devient alors -4ab)
ou selon ton explication
Philoux
OK merci. Je préfère ne pas dire "en faisant passer" pour éviter les erreurs de signes. De plus, les profs de maths n'aiment que l'on dise "en faisant passer" à cause des erreurs de signes justement.
Je dois aller en cours. Merci Philoux.
Je dois donc démontrer que
V(ab) < (a+b)/2
Je me pose une question :
ab < [ (a+b)/2 ]² car on met les 2 membres au carré
ou
ab < (a+b)/2 * V(ab) car on multiplie chaque membre par V(ab)
si A et B positifs et A < B alors A² < B²
si ton but est de faire disparaître les V, la seconde proposition ne t'avance guère 
Philoux


