Inscription / Connexion Nouveau Sujet
n! négligeable devant n^n
Bonjour à tous !
J'ai un problème dans un exercice qui me demande de démontrer n!<<n^n, et je n'arrive pas à conclure.
J'ai posé la suite Un=n!/n^n. Puis j'ai calculé U(n+1)/Un qui me donne (1+1/n)^(-n).
J'ai donc une suite croissante.
Puis je calcule la limite de U(n+1)/Un à l'aide des équivalences ce qui me donne : U(n+1)/Un--> e^(-1)
On a donc à partir d'un certain rang , Un+1/Un < e^(-1)
Un+1 < e^(-1)Un
Et voilà je suis bloqué. Si quelqu'un peut m'aider à conclure ça serait cool !
Merci d'avance.
bonsoir,
tu te casses bien la tête !
dans n! on fait le produit de tous les entiers jusqu'à n. Dans on fait la même chose sauf qu'au lieu de faire varier les facteurs de 1 à n , ils sont tous égaux au plus grand n. Y'a rien à démontrer. En plus, la suite que tu as définie n'est pas croissante :
déjà parce que (1+1/n)^(-n)<1 pour n>1 et également parce que si tu veux montrer que Un<1 il faut montrer qu'elle décroit de telle sorte qu'à partir d'un certain rang, elle soit en dessous de 1...
Autant pour moi Alexique je trouve Un+1/Un = ((n+1)/n))^n. Qui est supérieur à 1 pour tout n.
Ce qui y'a c'est que comme la limite de Un+1/Un est inférieur à 1 avec le théoreme de d'Alembert je pourrais dire que Un tend vers 0 et là je pourrais conclure mais je crois que mon prof veut pas que j'utilise ce théorème. Apres je pourrais aussi raisonner par l'absurde mais j'arrive pas à trouver une contradiction en supposant que la limite est non nulle.
Ton quotient Un+1/Un est toujours faux. Et gui_tou oui tu as raison (je viens de remarquer le double < d'Alien).
on peut faire simple aussi n^n=nxnxnxnxnxnxnxnxnxnx
n!=1x2x3x4x....xn
donc n^n>nxn! (tu divise l'un par l'autre et tu prend le premier therme n pour l'un 1 pour l'autre)
A partir d'un certain rang p, on a donc où
soit ,
...
Comme est fixé (il est déterminé par la donnée de a, arbitraire), et que a<1, on a bien que la suite
converge vers 0.
C'est "une démonstration" du théorème que ton prof refuse, mais c'est une démarche classique
Je propose ceci également (s'il est pas encore trop tard...): et on a montré (enfin gui_tou a montré) que
donc il existe un rang N tel que pour n>N on a
donc
. Voilà ! Ce résultat-là ne fait pas intervenir de théorèmes extraordinaires (en tout cas aucun sur les séries en l'occurence) donc ton prof devrait accepter ça.
ha ouais  effectivement! sauf que moi j'ai mis le
effectivement! sauf que moi j'ai mis le sous la flèche et toc ! (bah ça m'aura entrainé à écrire en latex au moins...). Mais pourquoi son prof refuserait cette preuve-là alors ? Sinon, il reste l'équivalent de Stirling mais faut le connaitre ou qu'il ait le droit de l'utiliser...
Bonjour à tous, 
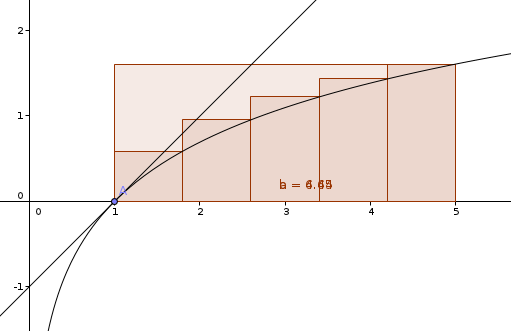
Juste pour proposer une vision géométrique. Passons au logarithme, il faut étudier .
est une somme de Riemann qui approche l'aire de
entre
et
avec une "finesse" de
(longueur du pas de la subdivision)
et avec une "finesse" de
(c'est un rectangle). Pour montrer ce que l'on veut il faut minorée l'aire de "l'escalier" restant par une fonction de
qui tende vers l'infini.
Quelque chose de simple est d'utiliser la concavité du logarithme : on considère la tangente en 1 (x-1) elle forme avec le rectangle un triangle "presque" (a une aire constante près) contenu dans l'escalier et d'aire
.
Tout ceci a été pensé sans papier ni crayon en moins de 30 secondes (pas peu fier)...donc il se peut que je me plante magistralement. 
Et est-ce qu'à ce stade de l'année Alien a vu les sommes de Riemann, la convexité ?...parce que moi non étant en sup également...
On m'avait introduit les intégrales en première (il me semble) en utilisant les somme de Riemann (sans en citer le nom). On peut les penser sans les citer. La concavité est une notion graphique ici l'inégalité utile peut se justifiée en dérivant.
A vrai dire ce qui m'intéresse n'est pas la rédaction (on peut toujours s'arranger et ici on peut s'arranger facilement) c'est ce que l'on voit : la représentation du problème.



 analyse en post-bac
analyse en post-bac