Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Nombres complexesTopics traitant de nombres complexes [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Nombre complexe.

Posté par
matheux14 31-03-21 à 05:30

Bonjour ,

Merci d'avance.

Dans les plan complexe rapporté à un repère orthonormé (O ;\vec{u} ;\vec{v}) , on considère les points A et B d'affixes respectives z_{A}=1+i et z_{B}=-\dfrac{1}{2}+\dfrac{1}{2}i.

On désigne par (C) le cercle de centre O et de rayon 1.

1) Donner la forme trigonométrique de z_{A} et z_{B}.

2) Dans la suite , M désigne un point de (C) d'affixe e^{i\alpha} , \alpha \in [0 ;2\pi[.

On considère l'application f qui a tout point M de (C) associe f(M)=MA×MB.

a) Montrer que \forall \alpha \in \R , e^{i2\alpha}-1=2ie^{i\alpha}\sin \alpha.

b) Montrer que : f(M)=\left|e^{i2\alpha}-1-\left(\dfrac{1}{2}+\dfrac{3}{2}i\right)e^{i\alpha\right|.

c) En déduire que : f(M)=\sqrt{\dfrac{1}{4}+\left(-\dfrac{3}{2}+2\sin \alpha\right)²}.

3-a) En utilisant 2-c) , montrer qu'il existe deux points M de (C) , dont on donnera les coordonnées , pour lesquels f(M) est minimale. Donner cette valeur minimale.

3-b) En utilisant 2-c) , montrer qu'il existe un seul point M de (C) , dont on précisera les coordonnées , pour lesquels f(M) est maximale. Donner cette valeur maximale.

Alors je bloque sur la question 2-c).

Posté par
Pierro236re : Nombre complexe. 31-03-21 à 06:31

Bonjour, c'est juste le calcul du module que tu as trouvé plus haut  . Donc pour ta question tu mets  le complexe sous forme a + ib et tu prends son module ça te fais donc |a+ib|=(a2 + b2) a étant la partie réelle et b la partie imaginaire.

Posté par
matheux14re : Nombre complexe. 31-03-21 à 10:03

Ah d'accord , merci

Posté par
lakere : Nombre complexe. 31-03-21 à 20:00

Bonsoir,

Nombre complexe.
J'ai bataillé tout l'après midi pour poster cette image "animée".
>> matheux14,

pour l'instant, tu dois totalement oublier les courbes plus ou moins ovoïdes en bleu et magenta.
Mais pour la suite, tu peux t'inspirer de cette figure.
Si tu es curieux, tu peux visiter ce lien :

Posté par
malou Webmasterre : Nombre complexe. 31-03-21 à 20:41

trop joli

Posté par
lakere : Nombre complexe. 31-03-21 à 20:46

Bonsoir malou,

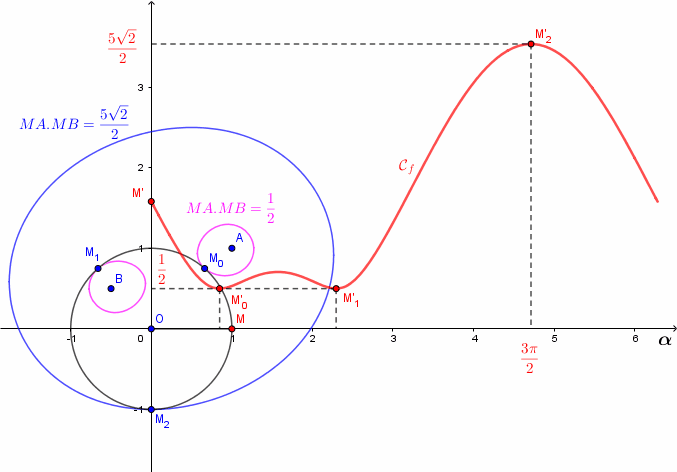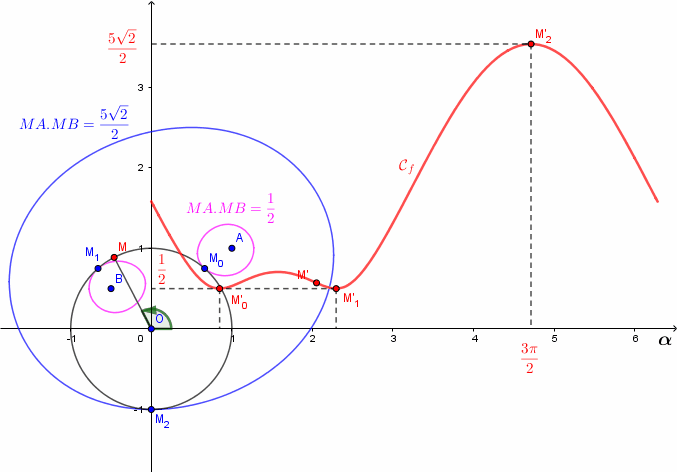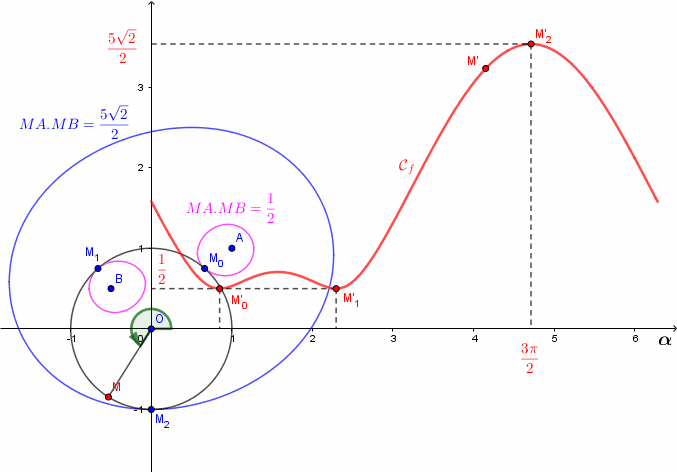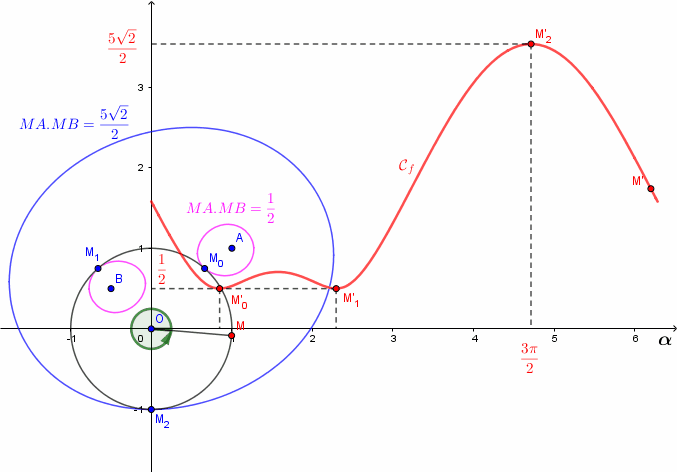
Ma figure est un peu "hermétique" mais c'est voulu : j'espère ici provoquer des interrogations multiples qui ne peuvent être que "positives" pour un élève de terminale.
Ceci dit, j'ai vraiment galéré pour poster une animation potable qui rentrait dans les clous du site

Posté par
matheux14re : Nombre complexe. 31-03-21 à 21:23

Bonsoir , ça se voit au sup ?

J'ai pas compris cette image..

Quel est l'intérêt ?

Posté par
lakere : Nombre complexe. 31-03-21 à 21:26

Bonsoir matheux14,

Alors pour l'instant, essaie de répondre à 3)a) et 3)b) sans te préoccuper de l'image.

Essaie d'éviter les dérivées dans les deux questions

Posté par
matheux14re : Nombre complexe. 31-03-21 à 21:35

Citation :

Essaie d'éviter les dérivées dans les deux questions


Ah c'est ce que j'avais voulu faire..

Du coup je fais comment pour étudier la fonction f~:~x\mapsto \sqrt{\dfrac{1}{4}+\left(-\dfrac{3}{2}+2\sin x\right)^{2}} \\ ?

Pour la question 2-c) , j'ai pu mais c'est très long..

Est ce le cas chez vous ?

Posté par
lakere : Nombre complexe. 31-03-21 à 21:49

Non, pas "très long" ...

Citation :
Du coup je fais comment pour étudier la fonction f~:~x\mapsto \sqrt{\dfrac{1}{4}+\left(-\dfrac{3}{2}+2\sin x\right)^{2}} \\ ?


Il y a un radical bien sûr mais on sait d'une part que le radicande (le carré d'un module et somme de deux carrés) est positif ou nul.

On sait aussi que la fonction racine est croissante sur [0,+\infty[

Étudier les variations de ta fonction f revient donc à étudier les variations de la fonction :

x\mapsto \left(2\,\sin\,x-\dfrac{3}{2}\right)^2+\dfrac{1}{4}

3)a) Pour quelle valeur de \sin\,x,  \left(2\,\sin\,x-\dfrac{3}{2}\right)^2+\dfrac{1}{4} est-il minimum ?

Posté par
matheux14re : Nombre complexe. 31-03-21 à 22:40

Comment auriez vous procédé ?

Moi j'ai procédé ainsi :

f(M)=\left|e^{i2\alpha}-1-\left(\dfrac{1}{2}+\dfrac{3}{2}i\right)e^{i\alpha\right|

En suivant le conseil de Pierro236 , je suis arrivé à e^{i2\alpha}-1-\left(\dfrac{1}{2}+\dfrac{3}{2}i\right)e^{i\alpha}=\dfrac{2(\cos(2\alpha)-1)-\cos\alpha+3\sin\alpha}{2}+i\dfrac{2\sin(2\alpha)-\sin\alpha-3\cos\alpha}{2}

Et j'ai montrer par calcul que \left(\dfrac{2(\cos(2\alpha)-1)-\cos\alpha+3\sin\alpha-2}{2}\right)^{2}+\left(i\dfrac{2\sin(2\alpha)-\sin\alpha-3\cos\alpha}{2}\right)^{2}=\dfrac{1}{4}+\left(-\dfrac{3}{2}+2\sin\alpha\right)^{2}.

Du coup f(M)=\sqrt{\dfrac{1}{4}+\left(-\dfrac{3}{2}+2\sin \alpha\right)²}.

3-a) \left(2\,\sin\,x-\dfrac{3}{2}\right)^2+\dfrac{1}{4} est minimale pour \sinx=\dfrac{3}{4}

Posté par
lakere : Nombre complexe. 31-03-21 à 23:19

On peut faire (un peu) plus court :

fM)=AM.BM=\left|(e^{i\alpha}-1-i)\left(e^{i\alpha}+\dfrac{1}{2}}-\dfrac{1}{2}\,i\right)\right|

f(M)=\left|e^{2i\alpha}-\left(\dfrac{1}{2}+\dfrac{3}{2}i\right)\,e^{i\alpha}-1\right|=\left|e^{i\alpha}\left[e^{i\alpha}-e^{-i\alpha}-\dfrac{1}{2}-\dfrac{3}{2}i\right]}\right|=\left|2i\,\sin\,\alpha-\dfrac{1}{2}-\dfrac{3}{2}i\right|

f(M)=\left|-\dfrac{1}{2}+i\left(-\dfrac{3}{2}+2\,\sin\,\alpha\right)\right|

f(M)=\sqrt{\dfrac{1}{4}+\left(-\dfrac{3}{2}+2\,\sin\,\alpha\right)^2}

Citation :
3-a) \left(2\,\sin\,x-\dfrac{3}{2}\right)^2+\dfrac{1}{4} est minimale pour \sinx=\dfrac{3}{4}


  oui pour \sin\,x=\dfrac{3}{4}

Je te rappelle que tu es passé de la variable \alpha à x

Après tout, pourquoi pas mais il ne faut pas l'oublier ...

  l'affixe des points M cherchés (pour ce minimum) est de la forme \cos\,\alpha+i\,\sin\,\alpha (qu'on te demande de déterminer).

  \alpha appartient à l'intervalle [0,2\pi[

\sin\,\alpha, on le connait maintenant : il vaut \dfrac{3}{4} mais sur l'intervalle précédent, il y a deux valeurs pour \cos\,\alpha (qu'il faut trouver) donc deux points M du cercle unité pour ce minimum.

Posté par
matheux14re : Nombre complexe. 31-03-21 à 23:42

\cos \alpha =0

Citation :
mais sur l'intervalle précédent, il y a deux valeurs pour \cos\,\alpha (qu'il faut trouver) donc deux points M du cercle unité pour ce minimum.


Je ne comprends pas vraiment..

Quel intervalle ?

[0 ; 2π[ ?

Posté par
lakere : Nombre complexe. 31-03-21 à 23:51

A ton avis ? Je cite ton énoncé :

  

Citation :
2) Dans la suite , M désigne un point de (C) d'affixe e^{i\alpha} , {\red \alpha \in [0 ;2\pi[}.


si \sin\,\alpha=\dfrac{3}{4}, que peut donc valoir \cos\,\alpha ?

Je te rappelle une célèbre formule :

   \cos^2\alpha+\sin^2\alpha=1

Posté par
matheux14re : Nombre complexe. 31-03-21 à 23:58

\cos\alpha=\dfrac{\sqrt{7}}{4}

Posté par
matheux14re : Nombre complexe. 31-03-21 à 23:59

Oui \cos\alpha=-\dfrac{\sqrt{7}}{4}

Posté par
lakere : Nombre complexe. 01-04-21 à 00:13

Oui, deux solutions et avec z_M=\cos\alpha+i\,\sin\,\alpha, tu obtiens deux points:

M_0 d'affixe \dfrac{\sqrt{7}}{4}+\dfrac{3}{4}\,i

M_1 d'affixe -\dfrac{\sqrt{7}}{4}+\dfrac{3}{4}\,i

Pour ces deux points qui correspondent au minimum, on te demande de le calculer, c'est à dire calculer f(M_0)=f(M_1) ...

Tu peux commencer à regarder la figure de 20h00 d'un peu plus près ...

Je dois quitter...

Posté par
matheux14re : Nombre complexe. 01-04-21 à 00:17

Bonne nuit.

Posté par
lakere : Nombre complexe. 01-04-21 à 00:22

Bonne nuit à toi matheux14


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !