Inscription / Connexion Nouveau Sujet
nombre complexe et geometrie
Bonjour a tous, j'ai un probleme avec cet exercice... je ne comprend pas comment est ce qu'on doit proceder pour le realiser, j'aimerais bien avoir une aide! merci d'avance!
On note H l'ensemble des points M(z) tels que z2-4=4- z barre 2
On note x et y les parties reelle et imaginaire de z.
1)a) Prouvez que M appartient a H si et seulement si x2-y2=4
b)Les points A, B, C ont pour affixes respectives:
a=2 , b=-3-i
5 , c= -3+i5.
Verifiez que A,B,C appartiennent a H.
2) ON note r la rotation de centre O et d'angle -
/4.
L'image du point M par r est le point M' d'affixe z'=x'+iy' (x'
,
y'.
a)Calculez les affixes a', b', c' de A',B',C'.
b)ON note H' l'ensemble des points du plan dont l'antecedent par r est un point de H. Exprimez x et y en fonction de x' et y' puis prouvez que M' appartient a H' si et seulement si x'y'=-2.
3)faites une figure sur laquelle vous placerez les points A,B,C,A',B',C' et la courbe H'. Construisez alors H.
------------------------------------------------------------------------------------------------
aidez moi SVP,ja'i trouvais le 1a mais apres je me suis bloquée.
MERCI
Bonjour,
Pour la question 1b: il suffit de vérifier si les nombres complexes, a,b,c remplissent la condition x²-y²=4. Tu dois pouvoir le faire.
Question 2a: La rotation de centre O et d'angle -/4 est caractérisée par le fait qu'un point quelconque M d'afixe z a son image M' d'affixe z' telle que :
Autrement dit on obtient :
Il ne te reste plus qu'à remplacer tout ça ... 
merci beaucoup patrice, ca ma beaucoup servie ton aide. Juste ue question est ce que lors de la question 2a c'est juste ce que j'ai trouvé: a'= 2e-i/4
b'= -3e-i/4-i5 e-i/4
c'= -3e-i/4+i5 e-i/4
ou il faut les developper plus, parce que apres pour les placer comment on fait, parce qu'on a par exemple a'= 2e-i/4.
et un petit truc pour la question 2b lorqu'il faut prouver que x'y'= -2, je ne sais pas trop comment faire. Aide moi s'il te plait
merci!
Pour a', pas de problème car on a sa forme trigonométrique (|a'|=2 et arg(a')=-/4. Il est donc facile de placer le point A' sur le cercle de centre O de rayon 2 et tel que .
En revanche pour les points B' et C', il faut trouver leur écriture trigonométrique, ou plus simplement, leur écriture algébrique :
e-i/4=
Il faut alors développer...
Cependant, si tu as bien compris que la multiplication par e-i/4 correspond à une rotation de centre O et d'angle -/4, alors tu peux construire les points A', B' et C' à partir des points A,B,C en utilisant un simple compas ... (mais la question est "calculer a', b', c' ...)
Pour la question 2b) il faut d'abord calculer x' et y' en fonction de x et de y. Sauf erreur on trouve :
.
Ensuite, il faut utiliser le fait que le point M d'affixe z=x+iy appartient à H si et seulement si x2-y2=4 ...
Excuse moi de te derenger encore une fois mais pour les affixes b' et c' je trouve des trucs tres bizares donc je peux pas les placer sur une figure j'ai deja pris 2/2 - i2/2 o lieu de e-i/4 et pour b' j'ai trouvé:
(2 (-3-5))/2 + (i2 (-5+3)/2
donc je me sens vraiment perturbée pour pouvoir le placer dans l'axe.
aide moi stp
merci d'avance!
Bonjour,
Ta réponse pour b' est juste. Il ne fallait pas t'attendre à un résultat très simple ... puisque le nombre b lui-même est compliqué.
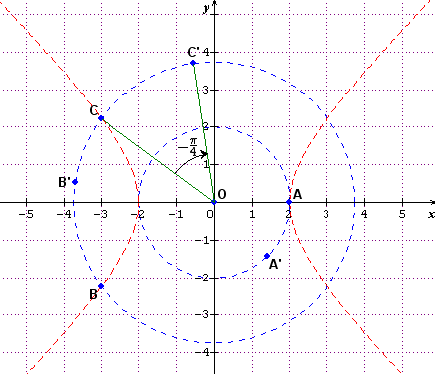
Voici une figure qui devrait t'aider :
en rouge, j'ai tracé la courbe d'équation x²-y²=4
en pointillés j'ai tracé les cercles de centre O passant par A d'une part et par B et C d'autre part.
Les im
Annuler
connectez vous