Bonjour !

Je vous donne l'énoncé de mon exercice et ensuite je vous explique mon petit problème.
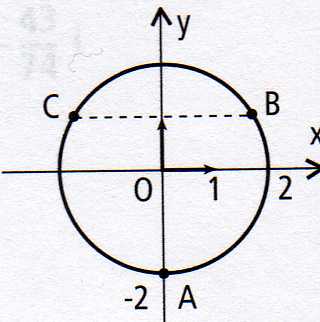
Donc : z²- 2i (z conjugué) = 0 ; pour cette question soit O, A, B. C les images dans le plan complexe, muni du repère orthonormal (O ; , ), des solutions obtenues. Montrer que le triangle ABC est équilatéral (où O a pour affixe zéro).

Je n'ai eu aucun problème à résoudre la première partie de l'énoncé.
J'ai donc obtenu O(0); A(-2i); B(3  +i) et C(-3  +i)
On a déjà un triangle isocèle en A puisqu'il y a symétrie orthogonale par rapport à (y'oy).

Je veux aussi le montrer d'une autre manière que AC = AB :
AC = |z_C- z_A|
AC = |-3  + i -(-2i)|
AC = |-3  + i + 2i|
AC = 3  + 3i (Me suis-je trompée dans les signes ?)

AB = |z_B- z_A|
AB = |3  + i + 2i|
AB = 3  + 3i

Ensuite il faut prouver que BC = AB
donc
BC = |z_C- z_B|
BC = |-3  + i - (3  + i)|
BC = |-23|

AB = 3  + 3i
C'est là que je ne comprends pas
comment 3  + 3i peut-il être égale à (3+9) ?

Pourriez-vous m'aider ?