Inscription / Connexion Nouveau Sujet
Nombre d'or
Bonjour voici un exercice auquel je ne comprend rien
1er partie: définition du nombre d'or
Le nombre d'or est le nombre irrationel noté par le lettre grecque o (prononcer phi) et égal à o = 1+V5 /2
Donne une valeur approchée a 10^-6 prés du nombre d'or
2ème partie construction géomètrique du nombre d'or
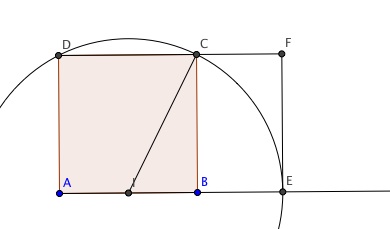
construis un carré ABCD de coté 1dm , on appelle I le milieu de segment AB
trace le cerle de centre I de rayon IC ce cercle coupe la demi droite de AB en E
Construis le rectangle AEFD
calcul IC puis démontre que AE=DF= 1+V5 /2
3ème partie le nombre d'or solution d'une équation
Montre que le nombre d'or est solution de l'équation x²-x-1=0
4ème partie le nombre dd'or dans la suite de Fibonacci
La suite de Fibonnasi est l'une des suites de nombres plus connus. Elle doit son nom au mathématicien Pisano .
Les 2 premiers termes étant 0 et 1 chaque terme suivant est la somme des deux thermes précedents voici donc les 7 premieres termes de la suite de Fibonacci 0 1 1 2 3 5 8 ...
a)continue cette suite de nombre jusqu'au 15ème terme
b) calcule de quotient du 12ème terme par le 11ème puis le quotient du 13ème terme par le 12ème, puis celui du 14ème par le 13ème et enfin le 15ème par le 14ème ? que constates-tu ?
c) à l'aide d'un tableau, calcule les 30 premiers termes de la suite de Fibonaci
d) calcule la suite des quotients obtenus en divisant un terme par son précédent, que constates-tu ?
5ème Partis : le nombre d'or dans une suite de fraction
voici une suite logique de fraction définie à partir du nombre 2 à l'aide du raisonnement "pour trouver la fraction suivante, je prends l'inverse de la précédente et j'ajoute 1 ". Cela donne :
F1= 2 F2= 1+(1/2) F3= 1+1/(1+1/2) F4 = 1 + 1/(1+(1/1+(1/2)))
F5 = 1+(1/F4)
écrire F1 F2 F3 F4 sous forme de fraction irréductible et donne pour chacune d'elle une valeur décimale approchée à 10-3 près. Que remarques-tu ?
Impressionnant ! Ce grand truc.
Courage et commence par le commencement.
partie 1
 = (1+
= (1+ 5)/2
5)/2
 =1, et des chiffres à arrondir
=1, et des chiffres à arrondir
Calculette et le 1 terminé.je regarderai
Partie 2
Tu peux quand même construire cette figure.
Prends bien les dimensions données.
Allez je regarderai
1)
1+V5/2 = 1.618033989
arrondi a 10^-6 = 1.618034
2)1dm=10cm
J'ai fait la figure est pour IC j'ai utilisé le théorème de pythagore dans AIC donc IC= 11.18 cm mais pour AE=DF=1+V5/2 j'arrive pas
bonjour,
question 1 OK
question 2 si tu veux aboutir à la réponse attendue, il faut garder des valeurs exactes (avec fraction et  )
)
AH oui j'ai oubliè de préciser que le rectangle AEFD est appelè rectangle d'or car la proportion entre se longueur et sa largeur est égal au nombre d'or
par d'accord pour IC
IC tu peux le calculer dans le triangle rectangle IBC
mais il faut garder la valeur exacte
IC2 = IB2 + BC2
IC2 = (1/2)2 + 12 = ....
Pour l'instant laisse tomber la figure.
Je vérifie .
Es tu sûre de l'énoncé ?
On retrouve bien le rectangle d'or et les bonnes proportions.
Mais c'est pas net.
Prends la question 3
Dans l'équation proposée si tu remplace les x par phi tu devrais trouver 0
Essaie
Pour Sephdar
Bonjour
Pour IC je trouve la même valeur que l'élève nous faisons surement une erreur dans la construction de la figure.
tu peux me joindre sur mon émail.
Merci
oui OK je n'ai pas fait attention à l'unité
IC vaut environ 1,1118 dm ou environ 11,18 cm
mais de toutes façons, il faut garder sous la forme IC = ( 5)/2
5)/2
Merci mais jette un oeil sur l'énoncé ca va pas.
On retrouve bien mon rectangle d'or mais les rapports demandés ne conviennent pas du tout.
Il faut vraiment que l'élève revoie le texte et le mieux c'est encore de sauter la question.
bon tu es prof je te laisse continuer puisque tu as pris la main.
GB
pourquoi "sauter" la question??
le texte est correct
la seule amélioration serait "trace le cerle de centre I de rayon IC, ce cercle coupe la demi droite [AB) en E"
Non j'ai vérifié il n'y a pas de faute dans l'énoncé
Si la 2ème partie pose problème on peut y revenir aprés et passer a la suite
En effet cette figure ne pose pas de problème puique on se retrouve bien avec un rectangle d'or.
Ce qui pose problème je le répète c'est cette phrase de l'énoncé qui pose problème.
calcul IC puis démontre que AE=DF= 1+V5 /2
Impossible !
Je suppose que l'énoncé est : calcul IC puis démontre que AE=DA fois 1+V5 /2
Pythagore est bon.
> gben
calcul IC puis démontre que AE=DA fois 1+V5 /2
c'est exact et ici AD = 1 (dm) c'est pour ça qu'il n'est plus dans le résultat
il faut que tu fasses le calcul en dm et pas en cm si tu veux retrouver la réponse proposée car elle est en dm
IC2 = IB2 + BC2
IC2 = (1/2)2 + 12
IC2 = 1/4 + 1
IC2 = 5/4
IC =  (5/4) = (
(5/4) = ( 5)/2
5)/2
AB = AI + IE or IE = IC
donc AB = AI + IC
AB = 1/2 + ( 5)/2 = (1+
5)/2 = (1+ 5) / 2
5) / 2
parce que j'ai encore fait une étourderie 
AE = AI + IE or IE = IC
donc AE= AI + IC
AE = 1/2 + ( 5)/2 = (1+
5)/2 = (1+ 5) / 2
5) / 2
tu pouvais aussi le trouver avec ce que tu as écrit
V1.25 = V5/4
IC = V1.25 = V(5/4) = (V5) / 2
pas d'accord
(1+V5/2)²- (1+V5/2) -1
identité remarquable
et signe - devant la parenthèse
et logiquement, tu dois trouver "0" au résultat
(pause pour moi)