Inscription / Connexion Nouveau Sujet
Nombre de sous-ensembles d'un ensemble (2^n)
Bonjour,
Voici un exercice que je dois faire et qui me pose problème:
"On veut prouver que le nombre de sous-ensembles d'un ensemble à n éléments est égal à 2n.
a) Donner un argument intuitif direct pour supporter cette affirmation (ne pas donner un exemple!).
b) Donner une preuve en utilisant le binôme de Newton."
Pour le point a), franchement j'ai beau réfléchir, j'ai cherché des tas de trucs sur internet, mais je vois vraiment pas ce qu'il y a d'intuitif là-dedans, et donc quel argument je pourrais donner. 
Pour le b), autant j'arrive à le démontrer par récurrence, autant avec le binôme de Newton j'ai un peu de mal...
En vous remerciant d'avance pour votre aide... 
Bonjour,
Pas très utile, ce que tu me dis là... concernant les 0 ou 1, j'ai déjà lu plein de choses sur Wikipédia ou ailleurs qui les citaient (y avait même des exemples avec des histoires de bits et compagnie), mais ça m'a plus embrouillée qu'autre chose... j'y connais rien en informatique... et en plus on est pas supposés donner des exemples 

Je suis perdue. 
Pas très utile, ce que tu me dis là...
c'est toi qui le dis.....
ce n'est pas un exemple
tu peux construire une application de ton ensemble de départ vers l'ensemble à 2 éléments {0;1} (ou bien "non", "oui") si tu préfères....et chaque sous ensemble est caractérisé par une application différente
donc il va y avoir autant de sous ensembles que d'applications possibles d'un ensemble à n éléments vers un ensemble à 2 éléments.....
Ok, je vois où tu veux en venir... mais en quoi cela permet-il de dire que le nombre de sous-ensembles sera égal à 2n?
Dans tous les cas, encore merci pour ta réponse... ça m'aide à y voir déjà un peu plus clair...!
n'as tu pas dans une vie antérieure appris à dénombrer le nombre d'applications d'un ensemble E vers un ensemble F dont tu connais le cardinaux ?
Dans une vie antérieure j'avais la pire moyenne de maths de ma classe et j'ai appris ce matin sur internet ce qu'était le cardinal parce que ce qu'on nous demande de faire comme exercices n'a même pas encore été vu en cours.
Donc non, désolée. Mais merci quand même pour ta réponse.
mais cela ne t'empêche pas de le faire avec le binôme de newton
tu comptes les parties ayant 0 élément choisi parmi n
tu comptes les parties ayant 1 élément choisi parmi n
tu comptes les parties ayant 2 éléments choisis parmi n
..
tu comptes les parties ayant n éléments parmi n
tu ajoutes tout
et tu trouves en réalité le développement de (a+b)^n avec a et b bien choisis...
bonjour,
Je vois que tu es du genre coriace.
Pour la partie intuitive Soit E={1,2,...,n)
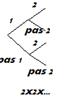
Pense à un arbre binaire, il y a les parties qui possèdent 1 et les autres qui n'ont pas 1, puis dans les deux cas précédents , il y a celles qui possèdent 2 et les autres qui ne possèdent pas 2 ..;etc
Bon... j'ai relu tout ce que vous m'avez écrit, j'ai encore cherché des infos sur internet...
Et franchement... je comprends mais vraiment plus rien du tout.  :(
:( 
C'est quoi une application qui va d'un ensemble de départ vers un ensemble d'arrivée? Evidemment j'arrive à concevoir ce qu'est une application qui va d'un ensemble E dans un ensemble F, par exemple, mais c'est quoi le rapport avec la donnée de mon exercice? Que signifie cette phrase de malou: "chaque sous-ensemble est caractérisé par une application différente"? Et pourquoi est-ce que tout ce qu'il (malou) a dit est supposé me permettre de dire "il va y avoir autant de sous ensembles que d'applications possibles d'un ensemble à n éléments vers un ensemble à 2 éléments"??
Et finalement: en quoi est-ce que le fait de comprendre tout ça est supposé me donner un argument INTUITIF DIRECT pour supporter cette affirmation??  :(
:( 
Je comprends vraiment plus rien du tout... je vois pas ce qui est supposé être intuitif (et direct!!) là-dedans... j'ai l'impression de faire du chinois...
En espérant que vous pourrez m'éclairer... 
Bon,
L'ensemble {1,2} quatre parties possibles: je ne prends rien
 ,{1},{2}{1,2} ,
,{1},{2}{1,2} ,
l'ensemble {1,2,3} ;les mêmes parties que {1,2} plus celles nouvelles dans lesquelles
entre le '3' ,c'est-à-dire plus { 3},{1,3},{2,3},{1,2,3}
Donc "ajouter un élément" revient à doubler le nombre des parties
...
Alain


 algèbre en post-bac
algèbre en post-bac