Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. PremièreForum de première NOMBRES COMPLEXESTopics traitant de NOMBRES COMPLEXES [tout]Lister tous les topics de mathématiques
Niveau première
Partager :

nombres complexes (2)

Posté par
nolimit76 12-02-12 à 00:04

On considère les nombres complexes suivants :

z1=\frac{3}{2}(\sqrt{3}+i) et z2=\bar{Z1}

1° Déterminer le module et un argument du nombre complexe z1, puis le module et un argument du nombre complexe z2.

2° Résoudre dans le système d'inconnues les nombres complexes z et z' :
        \left\lbrace\begin{array}l z-2z'=3\sqrt{3} \\ 2z-2z'=9i-3\sqrt{3} \end{array}  

3° Le plan complexe est muni d'un repère orthonormé (O;,) direct d'unité graphique 1cm.
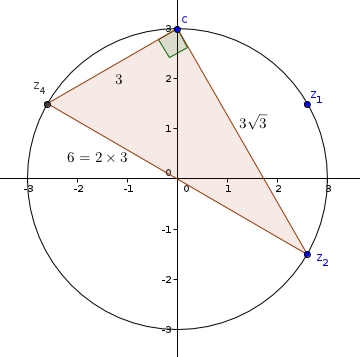
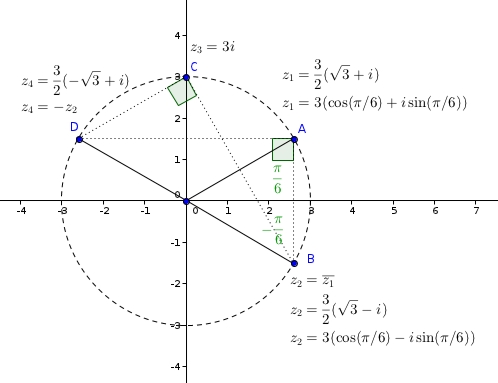
On considère les points A,B,C et D d'affixes respectives : z1, z2 3i et   \frac{3}{2}(-\sqrt{3}+i).

   a) Placer les points A, B, C et D.
   b) Démontrer que ces quatre points sont sur un cercle de centre O et de rayon à preciser.
   c) Construire puis justifier que le triangle BCD est rectangle.

            ______________________________________________________

                                  CORRIGE

1° z1=\frac{3}{2}(\sqrt{3}+i)
     =\frac{3\sqrt3}{2}+\frac{3i}{2}

  \mid z1 \mid= a²+b²
                         = \frac{\sqrt39}{2}

   Est ce que ce résultat est correct ?

Posté par
dhaltere : nombres complexes (2) 12-02-12 à 00:14

non

Posté par
nolimit76re : nombres complexes (2) 12-02-12 à 00:19

c'est z1 ou module de z1 qui est faux ?

Posté par
dhaltere : nombres complexes (2) 12-02-12 à 08:24

pourquoi voudrais-tu que z_1 soit faux ? c'est une donnée de l'énoncé, sauf si tu n'as pas recopié l'énoncé correctement, mais là, je ne peux rien pour toi.

z_1=\frac32(\sqrt3+i)

|z_1|=|\frac32|\times |\sqrt3+i|

|z_1|=\frac32\times \sqrt{\sqrt3²+1²}

|z_1|=\frac32\times \sqrt{4}

|z_1|=\frac32\times 2

|z_1|=3

z_2=\bar{z_1}

|z_2|=|\bar{z_1}| = |z_1| = 3

et pour l'argument, utiliser les autres formules du cours.

mais il y a beaucoup plus simple dans le cas présent : on peut directement faire apparaître module et argument

z_1=\frac32(\sqrt3+i)=3(\frac{\sqrt3}2+i\frac12)=3(\cos(\frac{\pi}6)+i\sin(\frac{\pi}6))

d'où
|z_1|=3 \\ \arg(z_1)=\frac{\pi}6\mod{2\pi}

|\bar{z_1}|=|z_1|=3 \\ \arg(\bar{z_1}) = -\arg(z_1)=-\frac{\pi}6\mod 2\pi

Tu abordes les nombres complexes en 1ère ?

Posté par
nolimit76re : nombres complexes (2) 12-02-12 à 12:45

Oui on a bientôt fini le chapitre

Posté par
nolimit76re : nombres complexes (2) 12-02-12 à 13:02

Heu pourquoi ta pas mis \frac{3}{2} dans la racine ? normalement on doit faire \mid z1 \mid=\sqrt{a²+b²} donc sa devrait faire \sqrt{(\frac{3}{2})²+(\sqrt{3}+\sqrt{1})²} ?

Posté par
nolimit76re : nombres complexes (2) 12-02-12 à 13:59

Posté par
dhaltere : nombres complexes (2) 12-02-12 à 14:28

Les complexes sont, dans le programme Français, abordés en Terminale.

Quel programme suis-tu ?

Quel retard as-tu dans la maîtrise des règles élémentaires de calcul ?

z=x+iy \\ |z|=\sqrt{x²+y²}

si tu veux te tenir à cette formule, alors l'expression initiale de z_1 ne convient pas

z_1=\frac32(\sqrt3+i)

n'est pas sous la forme
z=x+iy

Pour parvenir à cette forme, il faut développer
z_1=\frac32\sqrt3+i\frac32

et là, on identifie x=\frac32\sqrt3 et y=\frac32

alors on applique la formule, sans oublier les parenthèses :
|z_1|=\sqrt{(\frac32\sqrt3)²+(\frac32)²}

Allez, pour le fun, on réalise les calculs lourdingues(j'espère que ça te rafraîchira la mémoire) :

on développe les parenthèses
|z_1|=\sqrt{(\frac32)²\sqrt3²+(\frac32)²}

|z_1|=\sqrt{(\frac32)²3+(\frac32)²}

|z_1|=\sqrt{\frac{3²}{2²}\times3+\frac{3²}{2²}}

|z_1|=\sqrt{\frac{9\times3}{4}+\frac{9}{4}}

|z_1|=\sqrt{\frac{27+9}{4}}

|z_1|=\sqrt{\frac{36}{4}}

|z_1|=\sqrt{\frac{6²}{2²}}

|z_1|=\frac{\sqrt{6²}}{\sqrt{2²}}

|z_1|=\frac62

|z_1|=3

mais j'ai utilisé une autre technique, plus efficace

z_1=\frac32(\sqrt3+i) est un produit de deux nombres

or |a\times b|=|a|\times|b|

et donc

|z_1|=|\frac32|\times|\sqrt3+i|

|z_1|=\frac32\times\sqrt{\sqrt3²+1²}

|z_1|=\frac32\times\sqrt{3+1}

|z_1|=\frac32\times\sqrt{4}

|z_1|=\frac32\times\sqrt{2²}

|z_1|=\frac32\times2

|z_1|=3

ça te paraît simple ?

Posté par
nolimit76re : nombres complexes (2) 12-02-12 à 14:37

C'est plus clair pour moi.

En faite on étudie les nombres complexes mais pas vraiment en approfondie on a juste fait le conjugué, le module et argument + forme trigonométrique, représentation géométrique, et distance.

Posté par
nolimit76re : nombres complexes (2) 12-02-12 à 15:08

Pour le 2° je suis bloqué à 2z'=-93+9i

Posté par
nolimit76re : nombres complexes (2) 12-02-12 à 16:03

Posté par
dhaltere : nombres complexes (2) 12-02-12 à 17:34

oh, tu te calmes,

inutile de relancer 5 minutes après ton post

et si tu n'as pas de réponse immédiate, profites-en pour réfléchir.

Parce que c'est pas joli, joli

\left\lbrace\begin{array}l z-2z'=3\sqrt{3} \\ 2z-2z'=9i-3\sqrt{3} \end{array}  

si je retranche membre à membre la première équation de la seconde, j'obtiens :
(2z-2z')-(z-2z')=(9i-3\sqrt{3})-(3\sqrt{3})

et après simplification
z=-6\sqrt3+9i

après, j'ai un choix incroyable pour trouver z'

par exemple, reprenons la première équation
z-2z'=3\sqrt{3}

et remplaçons z par la valeur qu'on lui a trouvée
(-6\sqrt3+9i)-2z'=3\sqrt{3}

simplifions
-9\sqrt3+9i=2z'

et là, on arrive à ce qui te bloque.

retiens-moi : je divise les deux membres par 2. Sûrement une nouveauté pour toi.

\frac{-9\sqrt3+9i}2=z'

solution de ton système hyper compliqué :
\left\{\begin{array}{ccl}z&=&-6\sqrt3+9i\\z'&=&\frac{-9\sqrt3+9i}2\end{array}

Posté par
nolimit76re : nombres complexes (2) 12-02-12 à 18:31

Ok merci je l'ai refait pour voir si j'avais compris et c'est bon.

Ensuite pour la figure j'ai sa et il y a un truc qui cloche car logiquement les points A, B, C et D devraient être sur le cercle comme le dis la questions 3)b).

nombres complexes (2)

Posté par
dhaltere : nombres complexes (2) 12-02-12 à 18:58

nombres complexes (2)

je ne comprends pas pourquoi tu n'arrives pas à placer les points aux bons endroits.

tu remarqueras que z_4=-z_2, donc B et D sont symétriques par rapport à l'origine O

Il est clair que tous ces complexes ont même module.
|z_1|=3 \\ |z_2|=|\bar{z_1}|=3 \\ |z_3|=|3i|=3 \\ |z_4|=|-z_2|=3

ce sont donc les affixes de 4 points situés sur le cercle de centre O, l'origine du repère, de rayon 3

De plus, [BD] est un diamètre de ce cercle, donc le triangle BCD est rectangle en C, le triangle BAD est rectangle en A.

Posté par
nolimit76re : nombres complexes (2) 15-02-12 à 15:02

pour la 3)c j'ai un problème :

déjà pour les distances je trouve pour BD=6
                                       DC=\frac{\sqrt45}{2} et pareil pour BC. Il y a forcement un problème car quand on fait réciproque Pythagore
                        BD²=6²=36
                       DC²+BC²=(\frac{\sqrt45}{2})²+(\frac{\sqrt45}{2})²
                              =90/4    

c'est pas logique

Posté par
dhaltere : nombres complexes (2) 15-02-12 à 19:55

BD=6 : encore heureux, [BD] est un diamètre du cercle de rayon 3

B : z_2=\frac32(\sqrt3-i)
C : c=3i
D : z_4=-z_2=-\frac32(\sqrt3-i)

\begin{array}{ccl}DC &=& |c-z_4|\\ &=& |3i+\frac32(\sqrt3-i)|\\&=&|\frac32\sqrt3+i(3-\frac32)|\\&=&|\frac32\sqrt3+i\frac32|\\&=&\frac32|\sqrt3+i|\\&=&\frac32\sqrt{\sqrt3²+1²}\\&=&\frac32\sqrt{4}\\&=&\frac32\times2\\&=&3\end{array}

\begin{array}{ccl}BC &=& |c-z_2|\\ &=& |3i-\frac32(\sqrt3-i)|\\&=&|-\frac32\sqrt3+i(3+\frac32)|\\&=&|-\frac32\sqrt3+i\frac92|\\&=&\frac32|-\sqrt3+3i|\\&=&\frac32\sqrt{\sqrt3²+3²}\\&=&\frac32\sqrt{12}\\&=&\frac32\times2\sqrt3\\&=&3\sqrt3\end{array}

\begin{array}{ccl}\sqrt{DC²+BC²} &=& \sqrt{3² + (3\sqrt3)²}\\ &=& \sqrt{3²(1+3)}\\&=&3\sqrt4\\&=&3\times2\\&=&6 \\ &=&BD\end{array}

réjouis-toi, tu as encore d'immenses marges de progrès devant toi, ce qui est un bon départ pour tenter de progresser.

mais comme je te le disais, le résultat était prévisible, puisque, encore une fois, [BD] est un diamètre, et alors, c'est une propriété fondamentale vue au collège, pour tout autre point X du cercle, XBD est un triangle rectangle en X
nombres complexes (2)

Posté par
Ever82re : nombres complexes (2) 01-03-18 à 20:01

Alors désoler pour ce gros up, mais comment fait-on pour trouver que z2=z1barre=z1=3 ?

Posté par
Yzzre : nombres complexes (2) 01-03-18 à 22:00

Salut,

z2 = z1 barre : donné dans l'énoncé.
Mais ce sont leurs MODULES qui sont égaux à 3...
Suffit de les calculer.


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !