Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Nombres complexesTopics traitant de nombres complexes [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Nombres complexes

Posté par
E2NB 14-05-20 à 19:42

Bonjour à tous.
Je vous écris ce message pour vous demander de l'aide sur la résolution d'une équation.

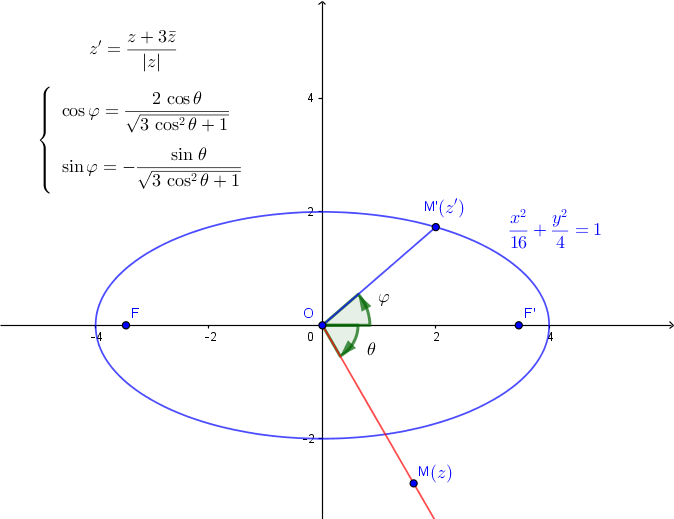
(E): z+3z(barre)=(2+i(3))|z|

J'espère que vous pourrez m'aider.

Posté par
E2NBre : Nombres complexes 14-05-20 à 19:43

Je ne sais pas comment procéder.

Posté par
Yzzre : Nombres complexes 14-05-20 à 19:54

Salut,

C'est pas très fun, comme équation.
Tu as essayé en remplaçant z par x+iy ?

Posté par
Armenre : Nombres complexes 14-05-20 à 22:04

*** Bonjour ***

En procédant comme le ditYzz tu peux établir dans un premier temps :
z+3\overline{z} \iff \left\lbrace\begin{array}  2x=\sqrt{x^2+y^2} \\ 2y=-\sqrt{3}\sqrt{x^2+y^2} \end{array}

***Edit Sylvieg : la politesse n'est pas optionnelle, aidant comme aidé***

Posté par
Armenre : Nombres complexes 14-05-20 à 22:06

Excuse : lire à gauche

z+3\overline{z}=(2+i\sqrt{3})|z|

Posté par
Armenre : Nombres complexes 14-05-20 à 22:13

Prudence pour la suite : l'élévation au carré des deux membres d'une équation n'est pas une transformation régulière, autrement dit on n'obtient pas une équation équivalente.
La seule chose que l'on puisse dire est : toute solution de l'équation f(x)=g(x) est nécessairement solution de l'équation \left(f(x)\right)^2=\left(g(x)\right)^2. Ce qui est déjà pas mal !

Posté par
Armenre : Nombres complexes 14-05-20 à 22:15

@Sylvieg.
Je pense que je vais arrêter de contribuer à ce forum ! Good Bye

Posté par
co11re : Nombres complexes 14-05-20 à 22:24

Bonsoir,
J'ai l'impression que ce n'est pas trop compliqué à résoudre même si peu sympathique au début.
Le système équivaut à :  2x = \sqrt{x² +y²}
                                                       y = -  2x 3

....

Posté par
Sylvieg Moderateurre : Nombres complexes 15-05-20 à 09:55

Bonjour,
@co11,
J'ai l'impression qu'il y a une coquille dans ton message.
Je penche pour enlever le 2 de la seconde égalité.

Posté par
matheuxmatoure : Nombres complexes 15-05-20 à 10:00

bonjour

(et surtout le changer de côté...)

Posté par
matheuxmatoure : Nombres complexes 15-05-20 à 10:23

ah non pardon j'ai confondu avec le système de départ

Posté par
co11re : Nombres complexes 15-05-20 à 12:18

Effectivement, le 2 est en trop. Merci sylvieg  

Posté par
lakere : Nombres complexes 15-05-20 à 13:01

Bonjour,

On peut aussi passer par la forme trigonométrique avec z=r(\cos\,\theta+i\,\sin\,\theta)

   z=0 est solution de (E)

si z\not=0,   (E)\Longleftrightarrow 4\cos\,\theta-2i\,\sin\,\theta=2+3i

  qui donne \theta=-\dfrac{\pi}{3}\;\;[2\pi]

Posté par
lakere : Nombres complexes 15-05-20 à 13:04

Une erreur:

   si z\not=0,   (E)\Longleftrightarrow 4\cos\,\theta-2i\,\sin\,\theta=2+i\,\sqrt{3}

Posté par
lakere : Nombres complexes 15-05-20 à 15:24

Un petit complément amusant en image:

  Nombres complexes

Posté par
E2NBre : Nombres complexes 19-06-20 à 01:35

Merci pour toutes vos explications et toutes vos esquisses, et désolé pour le retard. J'ai finalement pu résoudre cette équation en passant par une méthode de décomposition qui met en évidence l'argument r du nombre complexe ainsi que des cosinus et sinus (forme trigonométrique d'un nombre complexe).

Posté par
carpediemre : Nombres complexes 19-06-20 à 19:21

salut

avant d'élever au carré passer par le conjugué permet d'obtenir aisément les équations de Armen ...

en notant z* le conjugué de z = a + ib

z + 3z^* = (2 + i \sqrt 3) |z| \iff z^* + 3z = (2 - i \sqrt 3) |z^*|

donc par addition z + z^* = |z| => 4a^2 = a^2 + b^2 \iff (a\sqrt 3 - b)(a\sqrt 3 + b) = 0 \iff b = a \sqrt 3 $ ou $ b = -a \sqrt 3

et par soustraction z - z^* = -2i\sqrt 3 |z| => b^2 = 3(a^2 + b^2) \iff a = b = 0


PS : désolé pour les erreurs mais je ne peux pas faire d'aperçu car de gros pb de réseau et de temps de connexion ...

Posté par
lakere : Nombres complexes 20-06-20 à 21:43

Bonsoir carpediem,

Tu es coutumier du fait; je pourrais citer une centaine de topics où tu procèdes de la même manière; ici:

  

Citation :
donc par addition z + z^* = |z| => 4a^2 = a^2 + b^2 \iff (a\sqrt 3 - b)(a\sqrt 3 + b) = 0 \iff b = a \sqrt 3 $ ou $ b = -a \sqrt 3


  Tu enchaînes  une suite d'assertions logiques qui commencent par une implication et qui se poursuivent par des équivalences.
  Quand on est prof, je ne crois pas que ce soit la meilleure manière de présenter les choses; tes lecteurs lycéens ne voient plus que des équivalences là où la première implication fiche tout par terre. Didactiquement, est-ce bien raisonnable?
  De mon point de vue, si on commence par une implication, on continue par une implication (même si les équivalences suivantes sont justifiées) ne serait-ce que pour ne pas induire le demandeur en erreur.
  Je n'ose pas te soupçonner de malhonnêteté intellectuelle; tu ne balaierais tout de même pas les réciproques sous le tapis ?

Posté par
carpediemre : Nombres complexes 20-06-20 à 21:54

alors là je te rejoins bien sûr : j'aurai pu effectivement poursuivre par une suite d'implications et c'est ce que je fais régulièrement mais il a été dit plutôt que :

Armen @ 14-05-2020 à 22:13

Prudence pour la suite : l'élévation au carré des deux membres d'une équation n'est pas une transformation régulière, autrement dit on n'obtient pas une équation équivalente.
La seule chose que l'on puisse dire est : toute solution de l'équation f(x)=g(x) est nécessairement solution de l'équation \left(f(x)\right)^2=\left(g(x)\right)^2. Ce qui est déjà pas mal !
mon opération est du même ordre ... en travaillant d'abord dans les complexes plutôt que de passer immédiatement par la forme algébrique ... (quoique ici vient cela assez rapidement mais il est bon de travailler les complexes ... quand on travaille les complexes !!!)

d'autre part j'invite toujours (implicitement) le lecteur à penser ce qui est lu et non pas à lire ce qui est écrit ...


Rechercher
Menu
Espace membre
7 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1742 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !