Inscription / Connexion Nouveau Sujet
nombres complexes
bonsoir !
je bloque dans la deuxième question :
soit m un nombre complexe et on considère dans un plan orthonormé les points : M(m) B(-1+im) et C(-1-im)
1) determiner l'ensemble des point M(m) tel que M , B et C soient alignés . je trouve que c'est le cercle de centre G(1/2 ; 0) et de rayon r=1/4
2)on suppose que ImI^2 + Re(m) different de 0
soit R la transformation du plan qui associe M1(Z1) au point M'(Z') . montrez que R est une rotation en determinant son centre et un argument de son angle . mon intuition me dit que je dois penser au cercle de la question 1) mais je ne sais pas d'ou commencer .
Mais je pense que tu as une erreur ici:
je trouve que c'est le cercle de centre G(1/2 ; 0) et de rayon r=1/4
Oui le rayon est 1/2 , mais je pense pas que c'est normale de trouver un cercle lorsqu'il s'agit d'alignement... j'ai commencer par dire que M,BetC sont alignés equivaut à dire que le rapport (b-c)/m-c appartient à R ( b,c et m sont les affixes respectifs de B,C et M que j'ai cité )
<-> 2im/m+im+1 appartient à R <->2im/m+im+1 = -2×i×m(barre) / m(barre)-i×m(barre) +1 .... puis à la fin je trouve 2m×m(barre) + m + m(barre) =0 puis je pose m=x+iy avec (x;y)€ R ( l'euro ressemble au signe appartient 🙂) donc m(barre) = x-iy puis j'arrive à x^2 + y^2 + x=0 càd que (x+1/2 )^2 + y^2 = 1/4
Oui le rayon est 1/2
et pas seulement: le centre a pour coordonnées
j'ai commencer par dire que M,BetC sont alignés equivaut à dire que le rapport (b-c)/m-c appartient à R
Très bien (en n'oubliant pas les cas
J'avais écrit aussi:
Tu devrais revoir ton énoncé.
Parce que telle quelle, ta question 2) est incompréhensible...
Oui vous avez raison j'ai oublié de citer que Z'=iZ1 - 1 et au debut de la question j'ai dis que le module au carré de m + la partie réel de m est differente de 0 (je designe par " differente " toute la somme )
Z'=iZ1 - 1
Donc rien à voir avec la question 1)
Cherche le point invariant de
Oui, mais je ne sais pas ce que "tu sais":
Un transformation d'écriture complexe avec
et
est une rotation d'angle
et de centre le point invariant.
Si tu sais cela, la question est terminée. Mais le sais-tu ?
Ah moi je me suis lancé a essayer de trouver une expression comme Z' - w = e^i teta (Z1 -w) alors que c'est là 😅 .. donc ici le centre a pour affixe -(i+1)/2 et on a
-(i+1)/2 = racine carré (2)/2 × (1/racine carré (2) - i/racine carré (2) ) donc l'argument est -pi/4 c'est ça ?
Oui l'image du centre est lui même donc on conclut l'argument d'après l'ecriture algèbrique ou exponentielle de l'affixe du centre
Tu confonds (ici) et le point fixe d'affixe
(toujours ici).
Tu n'as pas répondu à ma question que je reformule:
Une transformation d'écriture complexe
Disposes-tu de la citation dans ton cours ?
Sinon, tu écris:
et par différence:
ou encore:
et tu te retrouves peut-être en pays plus "connu"

J'espère que ton exercice a une suite et que tu vas la poster (avec un retour qur la question 1))
Oui, mais je ne sais pas ce que "tu sais":
Un transformation d'écriture complexe
Non on a pas cette citation dans le cours ! Et est ce que c'est arg (z') au lieu de arg(a) dans votre citation ??
Si tu ne l'as pas dans le cours, tu n'as pas le droit de l'utiliser...
Et tu regardes au dessus à partir de:
Sinon, tu écris:
malou edit >*** Omarztoti, mets ton profil à jour, merci ! ***
Oui z'-w = e^ipi/2 (z1 - w) est mon pays connu hhh . Je vais poster la suite de l'exercice le plus tôt possible . Merci pour l'aide !!!
Rebonsoir !
La suite de l'exercice ( en fait il me restait que 2 question )
Après avoir etabli :
et par différence:
ou encore:
On nous demande de demontrer
l'equivalence : (c-m)/c-b appartient à iR
<--> ( |m|^2= Imaginaire de m ) . j'ai établi
l'équivalence (c-m)/c-b apartient à iR
<--> (-1-im-m)/-2im apartient à iR et puis
J'arrive à im -i×mbarre + 2m×mbarre =0
im -i×mbarre + 2(Re(m)^2 + Im(m)^2)=0
ensuite je remplace m et mbarre par x+iy
et x-iy avec x et y des réels et je trouve à la
fin que Re(m)^2 + Im(m)^2 = Im(m) de
l'autre part |m|^2= Im( m )<-->
( racine carré ( Re(m)^2 + Im(m)^2))^2=Im
(m) <--> Re(m)^2 + Im(m)^2 = Im(m) donc
L'equivalence est verifiée
Pour la dernière question question on
nous demande de déduire l'ensemble des
points M(m) pour que M,B,C et W( le
centre de la rotation R) soient cocycliques .
Je suis encore entrer de chercher la piste ...
Bonjour,
Remarque que:
demontrer
l'equivalence : (c-m)/c-b appartient à iR
<--> ( |m|^2= Imaginaire de m ) .
tu as montré que l'ensemble des points
est le cercle d'équation
Un dessin avec:
1) Le cercle bleu de la première question. (pour rappel).
2)Le petit cercle rouge de la seconde.
3)
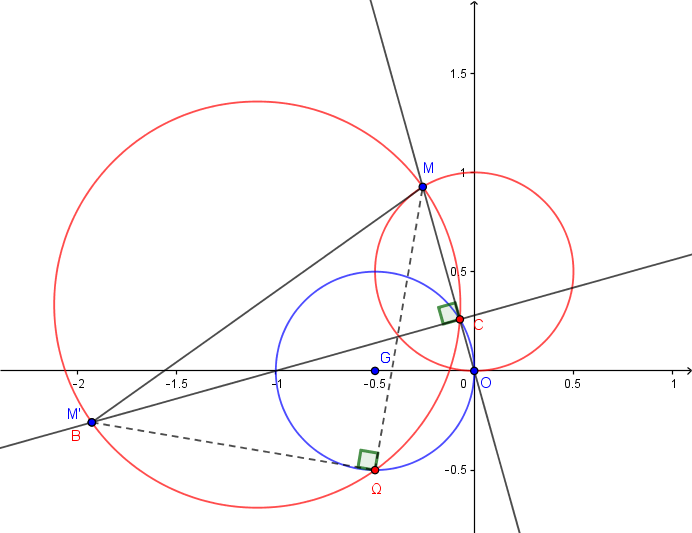
Il reste à réfléchir...

d'accord je comprends maintenant il fallait que je remarque le deuxième cercle. donc d' après l'équivalence qu'on a établi l'ensemble des points M pour que( MC )et (CB) soient perpandiculaires est le cercle d'eqt x^2 + y^2 -y = 0 donc M,B et C sont non alignés càd que M,B,C et W sont non alignés et comme b= im-1 donc d'après ce qui precède B=R(M) d'où (vec(CB) ; vec(CM) ) = (vec(WM) ; vec(WB) ) càd M,B,C et W sont cocycliques
Conclusion : l'ensemble des point M pour que M,B,C et W soient cocycliques est la droite perpandiculaire à (CB) en C . C'est ça ?
Conclusion : l'ensemble des point M pour que M,B,C et W soient cocycliques est la droite perpendiculaire à (CB) en C . C'est ça ?
Je vois que tu n'as pas compris:
On peut vérifier que
Donc
Pour que les 4 points
Conclusion ?




