Inscription / Connexion Nouveau Sujet
nombres complexes et plan complexe
Bonjour, voici mon exercice :
Le plan complexe est munit d'un repère orthonormal direct (O ;  ;
;  ) d'unité graphique 2 cm.
) d'unité graphique 2 cm.
On appelle A et B les points du plan d'affixes respectives a = 1 et b = -1.
On considère l'application f qui, à tout points point M différebts du point B, d'affixe z, fait correspondre le point M' d'affixe z' définie par ;
z' = (z-1)/(z+1)
1) Determiner les points M tels que M = f(M).
2) a. Montrez que, pour tout nombres complexes dufférents de -1 : (z'-1)(z+1)= -2.
b. En déduire une relation entre module de z'-1 et module de z + 1, puis entre arg (z'-1) et arg (z + 1) pour tout nombre complexe z différents de -1.
Traduire ces deux relations en termes de distances et d'angles.
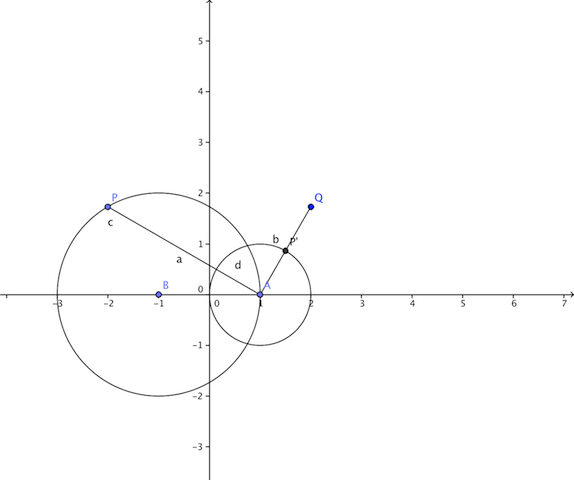
3) Montrer que si M appartient au cercle C de centre B et de rayon 2, alors M' appartient au cercle C' de centre A et de rayon 1.
4) Soit le point P d'affixe p = -2+iracine de 3.
a. determiner la forme exponentielle de (p+1).
b. Montrer que le point P appartient au cercle C.
c. Soit Q le point d'affixe q= - p "barre" ou p"barre" est le conjugé de p.
Montrer que les points A, P' et Q sont alignés.
d. En utilisant les questions précédentes, proposer une construction de l'image de P' du point P par l'application f.
dès la premiere question je suis bloquée, déja je ne comprend pas vraiment ce qu'ils veulent que l'on fasse... Pouvez vous m'aider ?
bonjour,
z≠-1
1) on te demande de trouver les points invariants
z'=z=(z-1)/(z+1)
tu résous z(z+1)-(z-1)=0
Determiner les points M tels que M = f(M).
si un point M d'affixe z est sa propre image alors z' doit être égal à z
je suis vraiment désolée mais je ne vois toujours pas ... Si M est égal à sa propre image je ne vois pas pourquoi son affixe devrais etre égale à l'affixe du point M' ?
les images des points A ,B,C et M sont nommées A' ,B', C' et M' c'est l'usage
un point invariant est sa propre image donc son affixe ne change pas
et on te demande de déterminer les ou le point(s) qui ont cette particularité
on les note M=f(M)
donc z'=z=(z-1)/(z+1)
j'ai cherché mais je ne trouve pas non plus... je ne vois pas comment démontrer avec z différent de -1 ...
tu ne dois pas démontrer que Z≠1
z doit être différent de 1 , c'est indiqué dans l'énoncé,valeur qui rend le dénominateur nul
tu dois démontrer que : (z'-1)(z+1)= -2 sachant que z'=(z-1)/(z+1)
tu calcules z'-1=(z-1)/(z+1) -1 = A
et ensuite A/(z+1) le résultat doit être -2
Moi je me retrouve avec z'-1 = -2/(z+1) ce qui n'est pas égal à l'aff(A)... Pouvez vous m'expliquer comment vous avez fait ?
Oui c'est bon j'ai trouvé !
Ensuite pour le b) la relation que j'ai trouvé entre les modules est la suivante : le produit des deux est égal à 2. Est-ce exact ?
ENsuite je ne vois pas quelle relation établir entre les arguments et je n'arrive pas a traduire en terme de distances...
Pouvez m'aider ?
Si je traduit ça en terme de distances je me retrouve avec DM' * DM = 2.
c'est correct ?
Ensuite pour les arguments j'ai chercheé mais je ne sais vraiment pas comment faire...
(z'-1)(z+1)= -2
|(z'-1)(z+1)|=| -2|=|z'-1|*|z+1|
et arg((z'-1)(z+1))=arg(z'-1)+arg(z+1)=0 [π]
AM'*BM=2
Ok
pour π [2π]
3) Montrer que si M appartient au cercle C de centre B et de rayon 2, alors M' appartient au cercle C' de centre A et de rayon 1.
traduis " M (z)appartient au cercle C de centre B(-1) et de rayon 2 " en langage mathématique
idem pour "M'(z') appartient au cercle C' de centre A (1) et de rayon 1."
Oui c'est bon normalement pour cette question je pense avoir réussit ;
On a BM = 2 et puis ensuite, grace à la formule trouvée dans la question précédente, on retrouve AM'= 1. Ce qui montre que...
Mais je suis bloqué a la question 4)c...
c. Soit Q le point d'affixe q= - p "barre" ou p"barre" est le conjugé de p.
Montrer que les points A, P' et Q sont alignés.
détermine q
calcule p'
puis montre que
c'est à la question suivante :"on te demande de trouver une construction pour le point P'"
pour la question 4c tu dois calculer l'affixe du point P' c'est à dire p'
d'accord, en revanche pour le calcul du quotient je trouve (i racine de 3 + 1)/2, ce qui n'est pas réel...
Q est le symétrique de P par rapport à l'axe des imaginaires
P' est à l'intersection de [AQ] et du cercle C' (A;1)
bonsoir, pouvez-vous m'expliquer la 3) dont je n'ai pas tout a fait compris le raisonnement? je vous en remercie d'avance!
Bonsoir deva3
3) Montrer que si M appartient au cercle C de centre B et de rayon 2, alors M' appartient au cercle C' de centre A et de rayon 1.
M est un point du cercle de centre B(-1) et de rayon 2
==>BM=2
à la question 2 tu as montré que (z'-1)(z+1)= -2==>
AM'.BM=2
d'où AM'=2/BM=1
par suite M' est sur le cercle de centre A et de rayon 1
Bonsoir, pouvez vous m'expliquer pourquoi on doit utiliser la formule (p'-a)/(q-a) pour montrer que les points A, P' et Q sont alignés dans la question 4.c)
Merci davance !

 [2
[2