Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Maths sup AnalyseTopics traitant de analyse [tout]Lister tous les topics de mathématiques
Niveau Maths sup
Partager :

Non continuité quantificateurs

Posté par
Ramanujan 03-07-18 à 02:59

Bonsoir,

Soit f une fonction de \R dans \R non continue en x_0

En présence de saut, dans une représentation graphique, il existe une quantité strictement positive \epsilon telle que l'on puisse trouver une abscisse x aussi proche voulue de x_0  pour laquelle on aura un écart entre f(x) et f(x_0) > \epsilon.

\exists \epsilon \in \R^{+*} , \forall \eta \in \R^{+*}, \exist x \in R, |x-x_0| \leq \eta \ et \ |f(x)-f(x_0)| > \epsilon

J'arrive pas à comprendre pourquoi c'est pas \forall \eta et \forall x

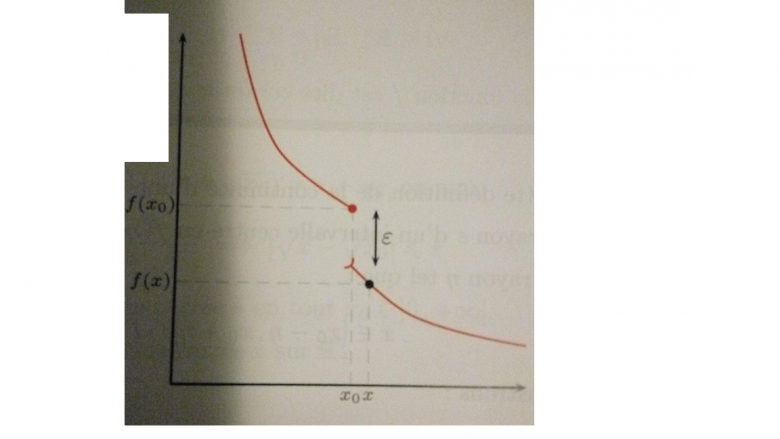
Non continuité quantificateurs

Posté par
Ramanujanre : Non continuité quantificateurs 03-07-18 à 03:05

Erreur de frappe , petite correction :

\exists \epsilon \in \R^{+*} , \forall \eta \in \R^{+*}, \exists x \in \R, |x-x_0| \leq \eta \ et \ |f(x)-f(x_0)| > \epsilon

En fait je comprends pas le quantificateur devant \x pourquoi c'est pas \forall x

J'ai du mal à comprendre pourquoi on met tel quantificateur dans cette définition je suis un peu perdu

Posté par
luzakre : Non continuité quantificateurs 03-07-18 à 08:12

Bonjour !
Tu veux écrire la négation d'une relation où il y a \forall x (écriture de la continuité). Il faut bien que cette négation comporte un \exists (à la place de x tu peux mettre une autre lettre si le x te gêne).

Posté par
etniopalre : Non continuité quantificateurs 03-07-18 à 08:22

Dire que f est  continue   au point a c'est dire qu'on a :  

smb]quelquesoit[/smb] > 0 on a P  où
P est  : > 0 tel que Q  où
Q  est  : x [a - , a + ]  on a R  où
R  est : |f(x) - f(a)|  <

Dire que f n'est pas  continue  au point a c'est donc dire qu'on a  :  

> 0 tq non P où
non P est  :    > 0 on a non Q  où
non Q  est :   x [a - , a +  ]  tq non  R  où
non R est  :  |f(x) - f(a)|     

Posté par
luzakre : Non continuité quantificateurs 03-07-18 à 11:37

Tu devrais compléter ton dessin en plaçant un intervalle [x_0-\eta,x_0+\eta et tu verras bien que l'inégalité n'est pas obtenue pour TOUS les x de cet intervalle.

Posté par
carpediemre : Non continuité quantificateurs 03-07-18 à 11:53

salut

il est quand même étonnant de ne pas voir que ce qui se passe à gauche et à droite de x_0 est totalement différent

à droite il y a évidemment continuité :  \forall e > 0  \exists n > 0  /  {\red \forall x}  :  x > x_0 $ et $ |x - x_0| < n => |f(x) - f(x_0)| < e

à gauche il n'y a pas continuité : \exists e > 0  \forall n > 0  /  {\red \exists x}  :  x < x_0 $ et $ |x - x_0| < n => |f(x) - f(x_0)| > e

Posté par
Ramanujanre : Non continuité quantificateurs 03-07-18 à 12:20

luzak @ 03-07-2018 à 08:12

Bonjour !
Tu veux écrire la négation d'une relation où il y a \forall x (écriture de la continuité). Il faut bien que cette négation comporte un \exists (à la place de x tu peux mettre une autre lettre si le x te gêne).


Oui je sais mais dans mon cours on introduit la continuité par un exemple de fonction non continue puis on donne la  définition de la continuité en faisant la négation de la non continuité.

Posté par
Ramanujanre : Non continuité quantificateurs 03-07-18 à 12:37

luzak @ 03-07-2018 à 11:37

Tu devrais compléter ton dessin en plaçant un intervalle [x_0-\eta,x_0+\eta et tu verras bien que l'inégalité n'est pas obtenue pour TOUS les x de cet intervalle.


Mon raisonnement est-il correct ?

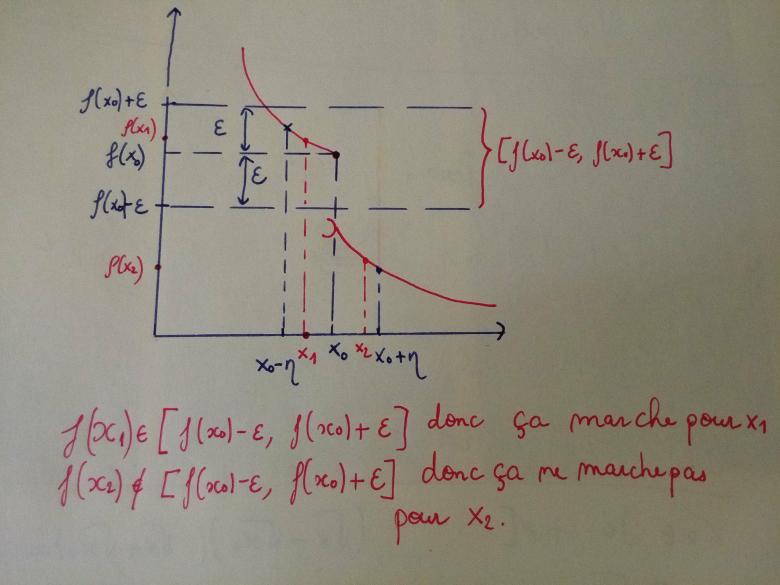
Non continuité quantificateurs

Posté par
Ramanujanre : Non continuité quantificateurs 03-07-18 à 12:50

Y a un petit détail qui me perturbe, sans partir de la définition de continuité mais en partant de mon énoncé, pourquoi dans la définition de la NON continuité c'est

\forall \eta \in \R^{+*} , \exists x \in \R^{+*} et pas  \exists \eta \in \R^{+*} , \exists x \in \R^{+*}

Posté par
luzakre : Non continuité quantificateurs 03-07-18 à 14:31

1. "ça marche ou pas" ne veut rien dire, sois précis !
2. un dessin peut aider mais tu ne peux pas, à partir de ton dessin, décider que "il existe \eta" aurait suffi à prouver la non-continuité.
3. "ton" énoncé" c'est quoi ? si tu veux traduire la non-continuité, il faut bien partir de la définition de la continuité.
Ce que tu fais c'est, à partir d'un dessin, montrer quelque chose de vraisemblable : cela ne suffit pas pour dire "non continue".

Posté par
Ramanujanre : Non continuité quantificateurs 03-07-18 à 21:12

L'auteur introduit la continuité de la façon suivante :

Il est facile de se faire une idée de ce qu'est une fonction continue ou non. Mais définir rigoureusement cette notion nécessite un peu d'attention.

Voyons pour commencer, ce qui se passe lorsque nous avons une fonction non continue en un point x_0 c'est-à-dire une fonction dont la représentation graphique présenterait une sorte de saut.

Il existe des abcisses x telles que :

1 / x est aussi proche que voulu de x_0

2/ |f(x)-f(x_0)| > \epsilon

Il utilise "il existe des x" donc on met \exists x \in R^{+*}

Après comment savoir à partir de cette explication qu'il faut mettre \forall \eta \in R^{+*} et pas \exists \eta \in R^{+*}  ?

Posté par
verdurinre : Non continuité quantificateurs 03-07-18 à 22:07

Bonsoir Ramanujan.
Tu proposes donc de dire que f définie sur un intervalle I contenant x0 n'est pas continue en x0 quand

\exists \varepsilon\in\R^{*+}\quad\exists \eta\in\R^{*+}\quad \exists x\in I \qquad |x-x_0| \leq \eta \ \text{et}\ |f(x)-f(x_0)| > \epsilon

Je propose I=\R,\quad  f\;:x\mapsto x^2\quad\text{et}\quad x_0=1.

En prenant

\varepsilon=\frac12,\ \eta=1 \text{ et } x=\frac13

on a bien

|x-x_0|<\eta car |\frac13-1|=\frac23 et \frac23<1

|f(x)-f(x_0)|>\varepsilon car |\frac19-1|=\frac89 et \frac89>\frac12

Donc, suivant ta définition, la fonction x\mapsto x^2 n'est pas continue en 1.
On voit assez bien ce qui ne vas pas.

Posté par
Ramanujanre : Non continuité quantificateurs 03-07-18 à 22:44

@Verdurin

J'ai compris votre contre exemple qui est bien vu.

Il faudrait que je trouve un \eta qui donne |x-x_0| \leq \eta ou |f(x)-f(x_0)| \leq \epsilon

Je peux prendre \eta = 0,1  et |x-x_0| \geq 0,1 donc f est continue en 1.

Mon raisonnement est juste ?

Posté par
mousse42re : Non continuité quantificateurs 03-07-18 à 22:50

Bonsoir,

Soit V_{x_0}, un voisinage de x_0.

Que l'on note V_{x_0}=]x_0-\eta, x_0+\eta[

Je pense que ce que veut dire l'auteur, c'est qu'on trouvera toujours un  x_1 \in V_{x_0}, tel que |f(x_1)-f(x_0)|>\varepsilon

"il existe des x aussi proches que voulu de x_0" <=> quelque soit ce voisinage, il existe un x dans ce voisinage..."

Posté par
verdurinre : Non continuité quantificateurs 03-07-18 à 22:59

@Ramanujan.
Quel raisonnement ?
Je n'en vois pas dans ton dernier message.
Le problème est dans la différence entre « pour tout » et « il existe ».

Le contraire de \forall x \ P(x) est \exists x \ \text{non}P(x)

Le contraire de \exists x \ P(x) est \forall x \ \text{non}P(x)

Posté par
Ramanujanre : Non continuité quantificateurs 03-07-18 à 23:12

mousse42 @ 03-07-2018 à 22:50

Bonsoir,

Soit V_{x_0}, un voisinage de x_0.

Que l'on note V_{x_0}=]x_0-\eta, x_0+\eta[

Je pense que ce que veut dire l'auteur, c'est qu'on trouvera toujours un  x_1 \in V_{x_0}, tel que |f(x_1)-f(x_0)|>\varepsilon

"il existe des x aussi proches que voulu de x_0" <=> quelque soit ce voisinage, il existe un x dans ce voisinage..."


Je comprends mieux sous cette angle pour chaque eta il existe un x différent dépendant de eta tel que....

Posté par
Ramanujanre : Non continuité quantificateurs 03-07-18 à 23:14

verdurin @ 03-07-2018 à 22:59

@Ramanujan.
Quel raisonnement ?
Je n'en vois pas dans ton dernier message.
Le problème est dans la différence entre « pour tout » et « il existe ».

Le contraire de \forall x \ P(x) est \exists x \ \text{non}P(x)

Le contraire de \exists x \ P(x) est \forall x \ \text{non}P(x)


Ah d'accord, je vois mais votre  contre exemple m'a bien montré que j'avais faux.

Posté par
mousse42re : Non continuité quantificateurs 03-07-18 à 23:24

Oui c'est ça !

pour l'exemple de verdurin que je salue, tu dois trouver un \eta qui est en fonction de \varepsilon

C'est à dire pour un \varepsilon>0 quelconque, et à partir de l'inégalité |x^2-1|<\varepsilon  trouver un \eta qui convient.

Posté par
Ramanujanre : Non continuité quantificateurs 03-07-18 à 23:41

J'ai : |x-1| \leq \eta

Donc si on prend : \epsilon = \eta ^2

|x^2 - 1| = |x-1||x-1| \leq \eta ^2

Posté par
mousse42re : Non continuité quantificateurs 03-07-18 à 23:43

|x^2-1|=

Posté par
Ramanujanre : Non continuité quantificateurs 04-07-18 à 00:02

mousse42 @ 03-07-2018 à 23:43

|x^2-1|=


Ah erreur de calcul : |x^2 -1| = |x-1| \times  |x+1|

Mais le |x+1| me gêne.

Posté par
mousse42re : Non continuité quantificateurs 04-07-18 à 00:15

On montre la continuité de f:x\to x^2 en x_0=1, c'est à dire que :

\forall \varepsilon>0, \exists \eta>0, \forall x\in \mathcal{D}_f, \quad |x-x_0|<\eta \implies |f(x)-f(x_0)|<\varepsilon

Soit \varepsilon >0

|x^2-1|<\varepsilon\iff |(x+1)(x-1)|<\varepsilon

On choisit un intervalle "qui va bien" autour de x_0, c'est à dire [0.5,1.5]

Ainsi on a sur cet intervalle  3/2|x-1|\le|(x+1)(x-1)|\le 5/2|x-1|

Dit autrement pour tout x\in[0.5,1.5], \;|f(x)-1|\le5/2|x-1|

On déduit de  |f(x)-1|\le5/2|x-1|<\varepsilon que |x-1|<\dfrac{2}{5}\varepsilon

On pose donc  \delta:= 2/5 \varepsilon.

Ainsi, si x \in]x_0-\delta, x_0+\delta[ \;\text{et}\; x\in [0.5,1.5], l'inégalité |f(x)-1|<\varepsilon est vérifiée.

Il suffit donc de poser \eta=\min\bigg\{\delta, 0.5\bigg\},

Posté par
Ramanujanre : Non continuité quantificateurs 04-07-18 à 01:08

Joli j'ai compris le raisonnement sauf la fin, les 2 dernière lignes.

Je comprends pas pourquoi il faut faire le Min avec 0,5 ?

En fait vous choisissez \eta = 0,5 dès le départ puis vous retrouvez un \eta = \frac{2}{5} \epsilon

C'est bizarre, j'ai jamais vu de raisonnement similaire.

Posté par
mousse42re : Non continuité quantificateurs 04-07-18 à 13:32

x\in[0.5,1.5], \;|f(x)-1|\le5/2|x-1|, cet intervalle permet de majorer la quantité |f(x)-1|

Ainsi il suffit que 5/2|x-1|<\varepsilon pour que |f(x)-1|<\varepsilon

Dit autrement :

\forall x\in[0.5,1.5], \quad 5/2|x-1|<\varepsilon\implies |f(x)-1|<\varepsilon

Maintenant on s'occupe de \quad 5/2|x-1|<\varepsilon dans [0.5,1.5]

5/2|x-1|<\varepsilon\iff |x-1|<\frac{2}{5}\varepsilon on gros cette inégalité est vraie pour tout  x\in]x_0-\frac{2}{5}\varepsilon, x_0+\frac{2}{5}\varepsilon[\cap[x_0-0.5,x_0+0.5]


Rechercher
Menu
Espace membre
15 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1730 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !