Inscription / Connexion Nouveau Sujet
nopmbre complexe forme exponentielle et nombre negatif
bonjour,
j'ai une petite question on me demande de mttre sous forme exponetielle
Z=-3e^(i /12)
/12)
j'ai bien repéré que -3 ne pouvait etre le module mais je ne sais pas vraiment quoi faire pour qu'il devienne positif.
voila si quelqu'un peut me donner un coup de pouce je le remercie d'avance
Bonjour,
Si tu ne souviens plus des formules, tu peux faire un ptit dessin.
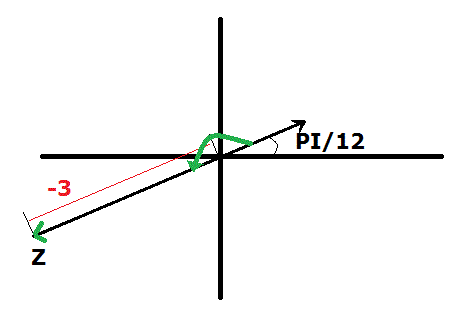
Le nombre Z et défini par un angle de PI/12 et par une "longueur" de -3. Donc, ca donne un truc comme ca.
Si tu veux avec un truc positif, il faut ajouter un demi tour à l'angle PI/12 (soit pi) et puis la "longueur" devient 3.
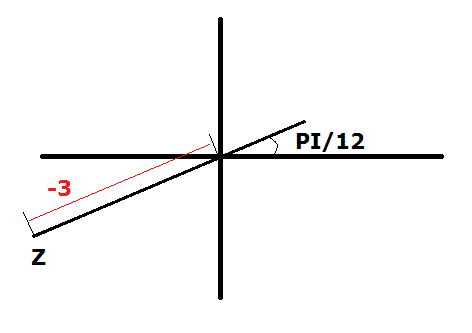
et bien merci beaucoup
si je comprends bien je dois simplement modifier l'argument pour retrouver une valeur positive du module ?
PS merci pour les schémas
Désolé je n'ai pas retrouvé le message que j'avais déjà envoyé!! donc je l'ai réecris à nouveau dans ce topic. Bonjour, je suis face à un problème rencontré dans mon DM de maths.... On a le nombre complexe z=(racine de 6+racine de 2 )+i(racine de 6-racine de 2)
Il faut que je détermine l'ecriture algébrique de z au carré. Par contre je trouve 8i. Ca me pose problème car ensuite je dois déterminer sa forme exponentielle et celle de z. Après cela, je dois trouver la forme exponentielle puis algébrique de z puissance 6, ensuite z puissance 9 puis de z puissance 12. Je n'arrive pas à réaliser l'exo, car mon résultat de départ me semble incorrect. Voulez vous bien m'aider s'il vous plait?? Merci d'avance
bonjour,
(R(6)+R(2))+i(R(6)-R(2))² est de la forme (a+ib)²=a²-b²+i2ab
Tout calculs faits, je trouve pas 8racine(3) + 8i
Je n'ai pas compris votre réponse. Car moi je trouve 8i, en appliquant la propriété que vous m'avez donnée, et vous, vous donnez 8racine 3+8i?
Je confirme le calcul...
(R(6)+R(2))+i(R(6)-R(2))²=(R(6)+R(2))²-(R(6)-R(2))²+2i((R(6)+R(2))*(R(6)-R(2))
(R(6)+R(2))+i(R(6)-R(2))²=6+2+2R(6)R(2)-(6+2-2R(6)R(2))+2i(6-2)=4*R(6)R(2)+8i=8r(3)+8i
Ahh merci beaucoup j'ai enfin compris l'erreur que j'avais commise. merci pour le détail des calculs.Par contre pour calculer avec les puissances de 6 9 et 12 existe -t-il une formule "facile" à traiter comme pour un carré?? Car il faut que je calcule z puissance 6, 9 et 12.