Inscription / Connexion Nouveau Sujet
Optimisation d'une aire. Niveau: Seconde G .
Bonjour à tous, je bloque sur un TP de mathématique depuis plusieurs jours et je vous demande votre aide.
L'énoncé:
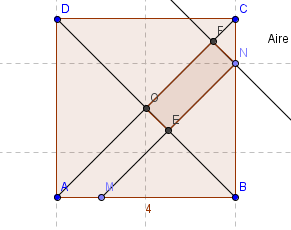
La figure ci-contre a les caractéristiques suivantes:
-ABCD est un carré de centre O et de côté 4;
-M est un point du segement [AB], distinct de A et de B;
-N est le point du segment [BC] tel que CN=AM;
-E est le point d'intersection des droites (MN) et (BD);
-F est le point d'intersection de la droite parallèle à la droite (BD) passant par N et de la droite (AC).
L'objectif de ce TP est de déterminer la position du point M permettant d'obtenir le quadrilatère ENFO d'aire maximale.
Étude algébrique:
1. a Quelle est la nature du quadrilatère ENFO ?
b Calculer la valeur exacte de OC
2. On pose AM=x et on considère la fonction F qui, au réel x, associe l'aire du quadrilatère ENFO.
Quel est l'ensemble de définition D de F ?
3. Quelle est la nature du triangle CFN ?
En déduire NF en fonction de x.
4. Calculer OF en fonction de x.
5. En déduire que:
F(x)=-1/2x2+2x
6. Étudier les variations de F sur D.
7. En déduire la position du point M pour laquelle l'aire du quadrilatère ENFO est maximale.
Que peut-on dire de ce quadrilatère pour cette position de M ?
8. a Montrer que chercher quand l'aire de ENFO est égale à 1/8 de l'aire de ABCD revient à résoudre l'équation:
x2-4x+4=0
b Résoudre par le calcul cette équation et confirmer ainsi votre conjecture de la partie A.
9. a Calculer l'aire du triangle CFN en fonction de x. Notons g(x) cette aire.
b Résoudre par le calcul l'inéquation f(x)>g(x)
c En déduire pour quelles valeurs de x, exactement, l'aire de ENFO est supérieur ou égale à l'aire de CFN.
J'ai beaucoup de mal a faire cette partie algébrique...
j'ai quand même réussi a trouver la valeur OC=4racine carré de2/2
et résoudre x2-4x+4=0 --> x=2
Mais pour tout le reste j'ai vraiment du mal...
Je vous demande donc de l'aide si il vous plait,
cordialement,
kiltas.
Bonjour,
nature du quadrilatère et nature du triangle c'est de la géométrie pas de l 'algèbre
donc tu as su faire ?
domaine de définition :
si M varie sur le segment [AB] donc entre A et B, et que AM = x, entre quelles valeurs varie x ?
NF en fonction de x : c'est encore un coup de Pythagore dans le triangle CFN dont tu connais CN = x ...
OF = OC - CF et "la nature du triangle" te donne CF.
l'aire est alors OF multiplié par FN, tout ça "en fonction de x" (c'est à dire écrit avec des "x" dedans, si c'est ça qui te bloque)
6) variations de f(x) : cours
etc...
PS : euh "et confirmer ainsi votre conjecture de la partie A" c'est quoi la partie A et surtout sa conjecture ??
Déjà merci de vos réponses, juste je suis très nul en géométrie je n'arrive pas a justifier correctement les natures des triangles etc...
La partie A fait référence a une partie réalisé sur GeoGebra la dessus il y a aucun problème.
je n'arrive pas a formuler avec x, pourtant j'ai un bon niveau en maths ^^ je sais très bien faire le théorème de Pythagore mais je n'arrive pas a l'exprimer avec ce x.
nature du quadrilatère : il suffit de prouver que MN est parallèle à AC
ce qui "coule de source" parce que les triangles BAC et BMN sont rectangle isocèles en B (BM = BN par différences de longueurs)
donc le quadrilatère est un parallélogramme et comme l'angle en O est un angle droit c'est fini.
pour le triangle CFN, qu'il soit rectangle en F découle de la question précédente
et comme l'angle en C est de 45° (diagonales du carré) il est rectangle isocèle.
(et par conséquent en découlera immédiatement NF = CN)
écrire "avec des x" est EXACTEMENT pareil qu'écrire avec d'autres lettres
tu sais bien écrire CN² = NF² + FC² non ?
et comme NF = FC (on vient de le justifier) CN² = 2NF²
et "avec des x" puisque CN = x dans l'énoncé : x² = 2NF²
et par conséquent NF² = .. et NF = ...
(avec les x qui restent des x, la racine carré de de x² c'est x, x multiplié par n'importe quel k c'est kx etc ...
manipulations élémentaires d'expressions algébriques, cours de 4ème, le calcul est exactement le même "formellement" que celui que tu as fait pour calculer OC)
la question 5 c'est aire = OF NF
NF
(ne pas confondre multiplier  et la lettre x
et la lettre x
comme c'est très peu visible la différence, on écrit * pour multiplier : aire = OF*FN)
tu viens de calculer OF et NF aux questions d'avant !
c'est du simple remplacement,
puis "développement élémentaires d'expressions algébriques, cours de 4ème" bis.
La partie A fait référence a une partie réalisé sur GeoGebra la dessus il y a aucun problème
(je ne vois pas comment on pourrait comparer quoi que ce soit à une conjecture dont on ne connait rien, vu d'ici hein)
Par cette missive, je tiens a te remercier de la diligence dont tu as fait preuve suite à ma requête de mathématiques.
Ton intervention de m'apporter ton aide a largement influencé le dénouement d'une situation fort délicate pour moi. Le problème est désormais réglé et c'est pour une grande part grâce à toi.
Puis-je te montrer demain ce que j'aurais réalisé afin que tu les juges ?
Avec toute ma reconnaissance.
Bien amicalement,
kiltas.
Bonjour,
Cette personne est quand même capable de demander à une personne de 4ème ce que veut dire "retrancher" en première réponse à un topic passant de sans réponse à message ayant reçu une réponse !

HS ici mébon puisqu'on en parle ...
passer du lyrisme à une aide laconique à ce point est effectivement surprenant et au final gênant
(c'était bien une aide à mon sens)
puisque la réponse était "retrancher veut dire qu'on effectue une soustraction"
et donc que
"ajoute 12
retranche la somme obtenue a 130"
veut dire qu'on calcule la soustraction 130 - le résultat précédent
c'était bien de l'aide !
même si maladroite et sans suite...
c'est surtout le "sans suite" qui est gênant, quand on intervient comme ça, on se doit de poursuivre effectivement l'aide, sinon le demandeur reste "le bec dans l'eau" vu que le topic n'est plus "rouge = non encore répondu"
et donc de répondre "rapidement" à la réponse de loulou28
Je n'ai fait cette remarque pour que tu comprennes et tu as compris ! tant mieux ! (la prochaine fois pense à ouvrir un dictionnaire !  )
)
ah d'accord, ce n'était donc pas de l'aide mais une demande d'explications de ta part sur le mot "retrancher" ...
(tu es étranger ?)
il n'empêche que ça a gravement perturbé le topic de loulou28, heureusement que jeveuxbientaider surveillait les topics même déja partiellement répondus ...
Non, je suis français et j'ai jamais vu ce mot en mathématiques durant toute ma scolarité ^^
Mais je suppose que cela doit dépendre des établissements fréquentés.
et en français ?
et dans le langage courant ?
faut pas s'accrocher "scolairement" à
cours de maths |séparation étanche| cours de français |séparation étanche| cours de ...
de toute façon la première réaction devant un mot inconnu est (doit être) effectivement d'invoquer le dictionnaire !! (en papier ou en ligne)
Effectivement je ne peux te donner tord
Bref ^^ je te souhaite une bonne nuit ou bonne soirée.
Demain je te montrerais mes résultats trouvés.
Je n'arrive pas a justifier correctement la nature du quadrilatère ENFO...
Est-ce correct ? ( bonne écriture)
2) D[0;4]
3)CN² = NF² + FC²
NF = FC
donc: CN² = 2NF²
x² = 2NF²
NF² = (√x2/2) et NF = x/√2
4) OF = OC-FC
OF = (4√2/2)- (x/√2)
5) aire = OF*FN
Aire = [(4√2/2)- (x/√2)] - (x/√2)
Je ne sais pas comment on arrive a obtenir F(x)=-1/2x2+2x ???
Les questions 6 7 et 9 toujours bloqués... 
pour ENFO j'ai pratiquement tout dit !!!!
nature du quadrilatère : il suffit de prouver que MN est parallèle à AC
ce qui "coule de source" parce que les triangles BAC et BMN sont rectangle isocèles en B (BM = BN par différences de longueurs)
donc le quadrilatère est un parallélogramme et comme l'angle en O est un angle droit c'est fini.
le reste est OK jusqu'à la question 5 où tu confonds multiplier et soustraire !!!
(et ensuite il te faut développer et simplifier)
la question 6 est "question de cours" directement en première (parce dans ce cours là il y a l'étude générale de la fonction f(x) = ax² + bx + c)
en seconde ce n'est pas "directement dans le cours" puisque la seule chose qui y est est les variations de la fonction f(x) = x² !
il faut donc se ramener à ça
ou bien reprendre la définition de "fonction croissante" et "décroissante"
de toute façon il faut, quoi qu'on choisisse de faire, ramener à ce qu'on appelle la "forme canonique"
c'est à dire que F(x) = -1/2x² + 2x = (-1/2)[x² - 4x] = -1/2[x² - 4x + 4 - 4]
identité remarquable pour x² - 4x + 4 = (x-2)²
et donc F(x) = (-1/2)[(x-2)² - 4]
et on peut alors "déduire" les variations de cette fonction de celles de Y = X²
(la question 7 est ensuite instantanée puisqu'il suffit de "lire" le tableau de variations de la question 6)
la question 9 eh bien on recommence selon le même principe pour calculer g(x) = CF*FN/2 = ... en fonction de x
puis l'inéquation se résout en mettant tout du même côté et en factorisant
on est alors amené à faire un tableau de signes de ce produit...
9) g(x)=x2/4
f(x)>g(x)
donc: (-1/2)[(x-2)² - 4] > x2/4
(-1/2)[(x-2)² - 4] - x2/4 > 0
-x(3x-8)/4 > 0
Est-ce correct ? je n'arrive pas a aller plus loin...
Pour le tableau de signes sa ira.
OK
et la seule chose qu'il reste pour aller plus loin est justement de faire le tableau de signes ...
(du produit des deux facteurs -x et 3x-8)
ah oui effectivement 
tu connais un petit site ou logiciel pour faire des tableaux de signes et variations ?
tu connais un petit site pour faire des tableaux de signes et variations ?
Ici : ..... ![]() [lien]
[lien]
tu connais un petit site ou logiciel pour faire des tableaux de signes et variations ?
ou si on veut le coder en LaTeX, effectivement le "micro-guide" LaTeX de l'ile
mais c'est pas ça qui va le remplir

En effet mon signalement de site te donne la solution pour nous envoyer un tableau de variations que tu as trouivé avec ton travail papier - crayon et que tu veux nous montrer !
Un site qui donne les variations sans réfléchir ne servant à rien, je ne te le donne pas !
ENFO n'est pas un carré.
il est un carré lorsque une certaine condition est réalisée : pour une certaine position de M bien précise, une certaine valeur de x bien précise. objet de la question 6 (les variations donc le maximum)
on t'a fait calculer NF et OF en fonction de x (questions 3 et 4)
donc tu peut savoir si pour cette valeur spéciale de x là on a NF = ON ou pas !


