Bonsoir,

qu'avez-vous trouvé pour la transformé de Fourier de  f(x)=x² ?

Bonsoir, je ne l'ai pas calculée... notre prof nous a dit que lorsque nous avons de coefficients réels, nous devons calculer a0, an et bn. puis a la fin, bien écrire la serie de fourier

autre chose :

votre fonction est paire donc les b_n sont nul.

oui, le professeur a raison.
Quand vous écrivez "Néanmoins, si l'on trace la fonction sur l'intervalle [0, 2π[," de quel fonction parlez-vous?

Bonjour,
Voici la représentation graphique de ma fonction. Or ici, on voit bien qu'elle n'est pas paire...

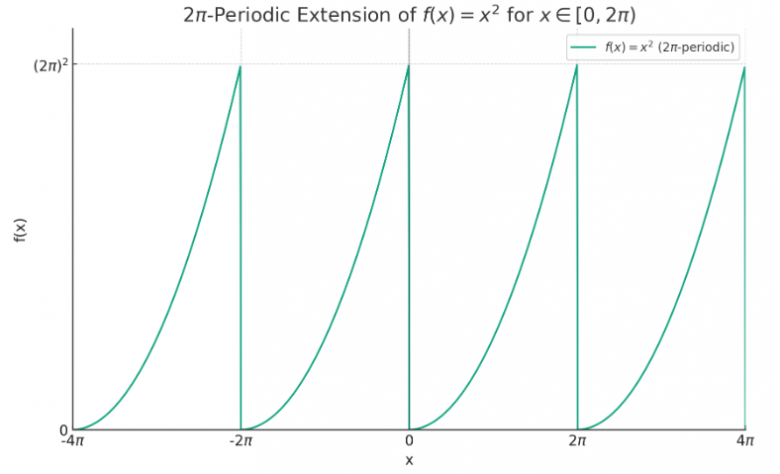
Bonjour,

f(x)=f(-x) ne suffit pas pour caractériser la parité, encore faut-il que le domaine de définition soit centré en 0.
Ici les b_n ne sont pas nuls.

@larrech,oups, j'ai été un peu vite, vous avez raison.

Bonsoir phyelec78; cela arrive à tout le monde. Du coup, plus de nouvelles de l'ami martizic

Re-bonsoir,
Merci beaucoup pour vos explications, je viens de finalement de comprendre! Donc, si j'ai bien compris, si nous avions eu f(x) = x^2 lorsque x ∈ à [-π, π[, alors la fonction aurait bel et bien été paire et donc bn = 0?

Oui, c'est cela

Merci beaucoup! Dernière question, est-ce que


Dans mon souvenir, si la fonction est 2π-périodique, alors on peut calculer les intégrales sur n'importe quel intervalle de longueur 2π. De plus, je crois également que sont paires donc on peut multiplier par 2 devant les bornes et réduire les bornes de l'intégrales.

Mon raisonnement est-il correct svp?

De plus, autre petite question qui me viens en tête, si nous trouvons que f est impaire, doit-on également vérifier que c'est sur un intervalle centré en 0? Par exemple, avec que f(x) sur [0, 2pi[, peut-on dire que an=0 ou alors vu que l'intervalle n'est pas centré, cela ne fonctionne pas?

Telle qu'elle est définie, la fonction f n'est pas paire.

Sur   elle n'est pas égale à   mais à

Donc ton calcul n'est pas correct. Il faudrait



quel intérêt ?

Pour qu'une fonction soit impaire, il faut également que son domaine de définition soit symétrique par rapport à l'origine.

Ainsi la fonction périodique égale à sur n'est pas impaire.

Ok merci beaucoup!

Par ailleurs, j'ai une autre question sur le théorème de Jordan-Dirichlet, mais je vais créer un nouveau sujet!

Merci pour votre aide sur celui-ci

Rebonjour,
Désolé de revenir sur le sujet, mais je viens de trouver un exercice qui m'a fait réalisé que je n'ai pas encore totalement compris le concept de parité.

Voici l'exemple en fonction :
Soit f : R -> R, une fonction 2π-périodique telle que f(x) = x² - 2πx, ∀x ∈ [0, 2π[

La première question de l'exercice est :
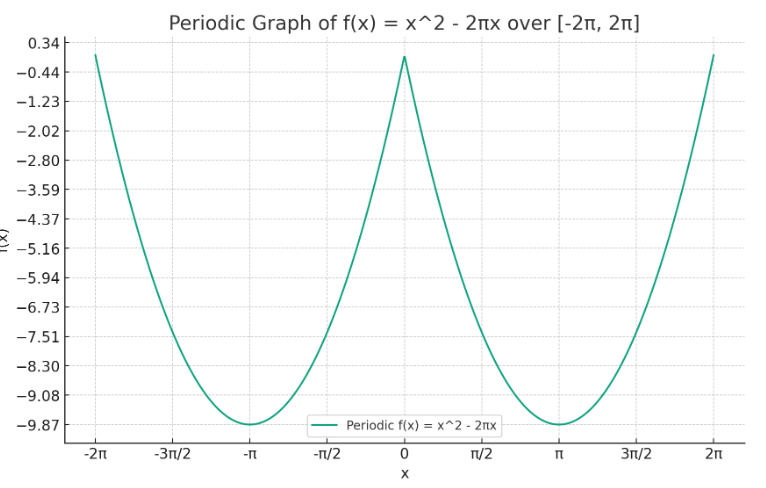
Veuillez tracer le graphe de f sur l'intervalle [-2π, 2π]. Puis, montrer que f est une fonction paire.

Veuillez voir ci-dessous le tracé de la fonction.

Or, graphiquement je vois que la fonction est paire mais je n'arrive pas à le démontrer...
1) La fonction est 2π-périodique mais l'intervalle est [0, 2π[, donc pas centré en 0.
2) f(-x) = (-x²) - 2π(-x) = x² + 2πx ≠ f(x)

@larrech pensez-vous pouvoir m'aider svp? Merci!

Oui, je n'ai pas été suffisamment précis dans mes réponses précédentes.

étant périodique, elle est définie sur tout intervalle inclus dans  . En particulier sur tout intervalle centré en l'origine d'amplitude un nombre entier de périodes.

C'est bien entendu un tel intervalle qu'il faut considérer pour évaluer la parité.

C'est bien d'ailleurs ce que tu avais fait instinctivement en traçant le graphe.

La question à se poser est donc : quel est le comportement de la fonction qu'on me propose sur, par exemple, l'intervalle [-T, T], T étant la période.

Je n'ai pas vraiment compris... donc pour savoir si f est paire ou impaire, je dois toujours tracer le graphique?

Je comprends que f peut-être paire sur un intervalle, mais lorsque j'affirmes que f est paire et donc bn=0, f doit-être pair sur quel intervalle dans mon cas? R entier ou [0,2π[ ou [-2π, 2π] ?

Pour évaluer la parité d'une fonction il faut commencer par se placer sur un intervalle symétrique par rapport à l'origine.

Regarde là par exemple ces quelques rappels

Pour une fonction périodique de période , tu peux prendre ou .

Une caractéristique de la parité est que sur un tel intervalle le graphe de la fonction est symétrique par rapport à l'axe des ordonnées. C'est donc un moyen simple de vérifier avant de le démontrer.

En ce qui concerne ton exemple. On se place sur .

Changement on obtient

Translation parallèle à d'amplitude on a  
devient

On obtient bien la même équation, donc parité.