Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... IUT/DUT AnalyseTopics traitant de analyse [tout]Lister tous les topics de mathématiques
Niveau IUT/DUT
Partager :

Parseval et résultat de Bâle

Posté par
kingst23 20-06-17 à 17:34

Bonjour on me demande de démontrer le résultat du problème de Bâle a l'aide de l'égalité de parseval ( utilisée pour la transformée de fourrier) présente sur l'image ci jointe.
On doit arriver a démontrer l'égalité présente dans le résultat du problème de Bâle soit que la somme de tous les 1/n² de 1 a +infini vaut π²/6.
J'aimerais s'il vous plaît une direction, un cap a suivre. Je n'ai pas réussi a arriver a quelque chose de concluant en simplifiant.

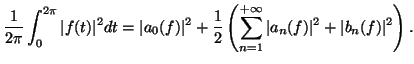
Parseval et résultat de Bâle

Posté par
luzakre : Parseval et résultat de Bâle 20-06-17 à 17:44

Bonjour !
Tu prends la fonction créneau :  f impaire, égale à 1 sur ]0,\pi[ et 2\pi-périodique, tu calcules les coefficients de Fourier et tu obtiens la série voulue (enfin, presque : il faudra écrire la somme des termes impairs et celle des termes impairs)...

Posté par
kingst23re : Parseval et résultat de Bâle 20-06-17 à 18:13

La fonction créneau est paire , non ?
La Dsf vaut 0.5+somme de n de 1 a + infini
De = (2sin(nt)/nπ)cos(nt)
Cela dit je vois toujours pas quel est le lien entre cette dsf et le résultat du problème de bale !
Merci de votre aide

Posté par
kingst23re : Parseval et résultat de Bâle 20-06-17 à 18:15

J'ai an =  (2sin(nt)/nπ)
BN=0 car fonction paire
oméga=1
A0=0.5
avec la fonction créneau

Posté par
luzakre : Parseval et résultat de Bâle 21-06-17 à 08:00

Tu fais ce que tu veux !
Je te dis de prendre une fonction impaire, et ça ne te plaît pas...Car tu as une idée arrêtée sur le mot "créneau". Oublie le mot et fais un dessin pour la fonction que je te propose.

Comment un coefficient  de Fourier peut-il contenir la lettre t ?

Posté par
kingst23re : Parseval et résultat de Bâle 21-06-17 à 09:54

Je l'ai fait mais du coup je me rends compte que l'intégrale de -pi a -pi de f est nulle car f est impaire. Je me mets sur le calcul !

Posté par
luzakre : Parseval et résultat de Bâle 21-06-17 à 10:20

Si tu parles du premier membre de la relation de Parseval, il s'agit d'intégrer la fonction strictement positive f^2. L'intégrale n'est pas nulle...

Si tu veux d'autre aide, merci de donner la valeur trouvée pour les coefficients de Fourier.

Posté par
larrechre : Parseval et résultat de Bâle 21-06-17 à 10:27

Bonjour,

kingst23 @ 21-06-2017 à 09:54

Je l'ai fait mais du coup je me rends compte que l'intégrale de -pi a -pi de f est nulle car f est impaire. Je me mets sur le calcul !


Oui, mais celle de |{f(x)}|^2} ne l'est pas

Posté par
kingst23re : Parseval et résultat de Bâle 21-06-17 à 11:34

Alors luzak j'ai
An=0 car fonction impaire
Bn=4/(n*Pi)

Posté par
kingst23re : Parseval et résultat de Bâle 21-06-17 à 12:07

J'arrive a légalité de parseval suivante:
4Pi²/3=1/2 * somme de 1 a +inf de 16/(n²*Pi²)
donc
8Pi²/3=somme de a 1 +inf de 16/(n²*Pi²)
puis
8Pi²/48=somme de a 1 +inf de 1/(n²*Pi²)
Pi²/6=somme de 1 a +inf de 1/(n²*Pi²)
J'y suis preque il y'a un facteur 1/Pi² dans la somme qui est genant...
Je vais revoir mes coefficients

Posté par
luzakre : Parseval et résultat de Bâle 21-06-17 à 12:23

Ton coefficient b_n est faux.
Tu devrais trouver b_{2n}=0,\;b_{2n+1}=\dfrac4{(2n+1)\pi} et \sum_{n\geqslant0}\dfrac1{(2n+1)^2}=\dfrac{\pi^2}8.

Ensuite tu utilises -je te laisse le soin de justifier et de mettre les bornes -

\sum\dfrac1{n^2}=\sum\dfrac1{(2p)^2}+\sum\dfrac1{(2p+1)^2}

Posté par
kingst23re : Parseval et résultat de Bâle 21-06-17 à 12:30

Je vais m'en occuper !
Cela dit que représente p dans ta dernière formule ?

Posté par
luzakre : Parseval et résultat de Bâle 21-06-17 à 17:42

Quand n est pair, je le note 2p...
Maintenant, si tu préfères
\sum\dfrac1{n^2}=\sum\dfrac1{(2n)^2}+\sum\dfrac1{(2n+1)^2}

Posté par
kingst23re : Parseval et résultat de Bâle 21-06-17 à 19:41

Je t'avoue que je n'avais jamais vu cette formule auparavant.

Posté par
kingst23re : Parseval et résultat de Bâle 21-06-17 à 19:57

On est d'accord que bn=2/T * integrale de -pi à pi de f(t)*sin(t) ?
bn=2/T * [ ( integrale de -pi à 0 de -sin(t) )+ ( integrale de 0 à pi de sin(t)  )]

Posté par
luzakre : Parseval et résultat de Bâle 22-06-17 à 08:13

Non, b_n=\dfrac2{\pi}\int_0^{\pi}f(t)\sin(nt)\mathrm{d}t quand f est impaire, 2\pi-périodique.

Pour ce qui est de la série, je t'avais invité à mettre les sommations :
\sum_{n>0}\dfrac1{n^2}=\sum_{n\text{ pair}}\dfrac1{n^2}+\sum_{n\text{ impair}}\dfrac1{n^2} (en justifiant les convergences)
\sum_{n>0}\dfrac1{n^2}=\sum_{n>0}\dfrac1{(2n)^2}+\sum_{n\geqslant0}\dfrac1{(2n+1)^2}
Que tu changes ou pas la lettre muette n en p,q,\text{wafwaf} ne change rien aux calculs.


Rechercher
Menu
Espace membre
9 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1742 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !