Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Maths sup AlgèbreTopics traitant de algèbre [tout]Lister tous les topics de mathématiques
Niveau Maths sup
permutation d'ordre 14 dans S10
Posté par robby3
Bonjour à tous,
Voici l'énoncé:
Citation :
Soit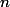 un entier
un entier  ,
,  un entier
un entier 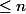 et
et  des éléments de
des éléments de ) .
.
1) Montrer que(x_1 x_r)=(x_2...x_r)=(x_1 x_2)(x_1...x_r))
2) En déduire une expression de la signature d'un cycle en fonction de sa longueur et deux façons d'écrire le cycle) comme produit de transpositions.
comme produit de transpositions.
3) Montrer que toute permutation d'ordre 14 de est impaire.
est impaire.
Soit
1) Montrer que
2) En déduire une expression de la signature d'un cycle en fonction de sa longueur et deux façons d'écrire le cycle
3) Montrer que toute permutation d'ordre 14 de
C'est bon pour 1) et 2) mais je ne comprends pas le lien avec 3...
Voilà ce que j'ai commencé à faire:
Si je prends une permutation d'ordre 14 dans
Comme j'ai pas 36 façons de faire 14, j'imaginais qu'il y avait une transposition (d'ordre 2) et un cycle d'ordre 7 et donc la signature d'une transposition c'est -1 et la signature d'un 7-cycle c'est
Mais par exemple, pourquoi la permutation d'ordre 14 ne se décompose-t-elle pas en un seul cycle d'ordre 14 ? Est-ce que c'est impossible car on est dans
Est-ce que mon raisonnement est correct ?
Merci d'avance de vos remarques !

Bonjour
Comment veux-tu avoir un cycle de longueur 14 alors que tu n'as que 10 éléments?
Utilise les décompositions possibles d'une permutation d'ordre 14 et utilise la première question.
Bonjour Camélia,
oui, ok, je crois que j'ai compris.
Une permutation d'ordre 14 ne peut se décomposer qu'en un cycle et une transposition.
Une transposition est d'ordre 2 donc le cycle est d'ordre 7
Et il ne peut y avoir qu'une seule transposition.


 algèbre en post-bac
algèbre en post-bac