Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Maths sup AnalyseTopics traitant de analyse [tout]Lister tous les topics de mathématiques
Niveau Maths sup
Partager :

Petit DL

Posté par clemence (invité) 04-09-07 à 08:54

Bonjour, pouvez-vous m'aider pour ce DL qui me pose problème ? Merci !

f(x) = 1/(1-x) * e(1/(1-x))

Posté par
mikayaoure : Petit DL 04-09-07 à 09:23

bonjour clemence

c'est au voisinage de 0 ton DL ?

si oui, dans ce cas 1/(x-1) tend vers 1 => pense que ex = e.ex-1

A toi

Posté par
mikayaoure : Petit DL 04-09-07 à 09:25

pardon sur l'exposant : ex = e.ex-1

A quel ordre est demandé ton DL ?

Posté par
mikayaoure : Petit DL 04-09-07 à 10:47

je me limite à l'ordre 2 et te propose ceci ( y'a peut-être plus sioux... )

comme exp(h) = 1 + h + h²/2 + o(h²) alors exp(x-1) = 1 + (x-1) + (x-1)²/2 + o( (x-1)² ) au voisinage de 1 et donc

le DL2 de exp(x) = e[1 + (x-1) + (x-1)²/2 + o( (x-1)² ) ] au voisinage de 1

le DL2 de 1/(1-x) = 1 + x + x² + o(x²) au voisinage de 0

d'où le DL2 au voisinage de 0 de exp( 1/(1-x) ) = e[1 + (x+x²) + (x+x²)²/2 + o(x²)] = e[1 + x + 3x²/2 + o(x²)]

il suffit ensuite de multiplier ce DL2 avec celui de 1/(1-x) :

DL2 = (1+x+x² + o(x²))(e(1+x+3x²/2 + o(x²)))


DL2 = e(1 + 2x + 7x²/2 + o(x²) ) au voisinage de 0


A vérifier cependant, je n'en suis pas certain ( si Dremi passe par là )

Quant au terme général, je jète l'éponge

Posté par clemence (invité)re : Petit DL 04-09-07 à 11:02

Merci, c'était bien à l'ordre 2 en effet et c'est ce que j'avais trouvé ! Pourtant l'étude de la fonction est étrange ensuite...enfin, tant pis ! Merci beaucoup !

Posté par
mikayaoure : Petit DL 04-09-07 à 11:03



attend peut-être l'avis de cadors qui te donneront d'autres méthodes plus adéquates...

Posté par
mikayaoure : Petit DL 04-09-07 à 11:26

en effet, particulière, la fonction

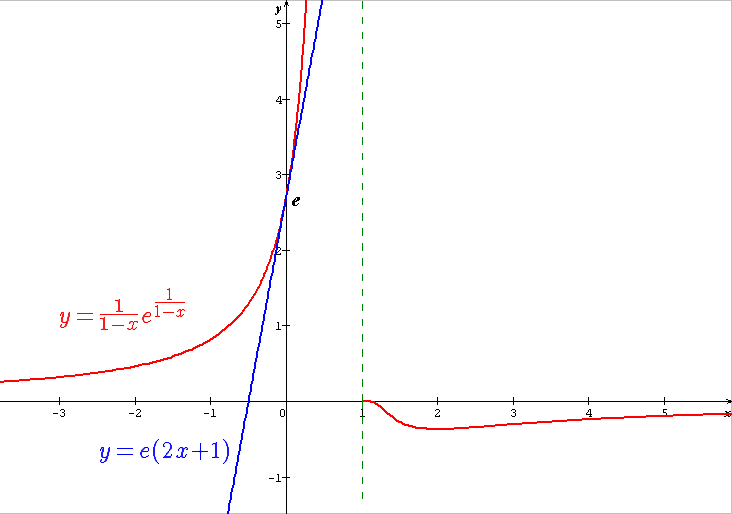
Petit DL

Pour revenir au DL, je me demande si on ne peut pas utiliser celui de Xexp(X) au voisinage de 1 ?

Posté par
kaiser Moderateurre : Petit DL 04-09-07 à 15:17

Bonjour à tous

mikayaou > je ne suis pas Dremi (désolé ), je ne me considère pas comme un cador mais je vais tout de même répondre à ce post !

je suis d'accord avec ton DL et j'aurais fait la même chose.

Citation :

Pour revenir au DL, je me demande si on ne peut pas utiliser celui de Xexp(X) au voisinage de 1 ?


D'abord, ça serait plutôt \Large{xe^{\frac{1}{x}}}, non.
Ensuite, utiliser un DL ailleurs qu'en 0 est peut-être un peu plus corsé.

Kaiser

Posté par
kaiser Moderateurre : Petit DL 04-09-07 à 15:20

Non, oublie ce que j'ai dit à propos de \Large{xe^{{\frac{1}{x}}} !
En fait, il faudrait plutôt \Large{\frac{1}{x}e^{{\frac{1}{x}}} (on est en effet forcé de passer par le DL de 1/(1-x)

Kaiser

Posté par
mikayaoure : Petit DL 04-09-07 à 15:26

merci kaiser

t'es trop modeste !

Dremi, toi et d'autres ( elhor, cauchy, raymond... ) proposent souvent de très belles résolutions, très ingénieuses; continuez !

Posté par
kaiser Moderateurre : Petit DL 04-09-07 à 15:27

merci !

Posté par
kaiser Moderateurre : Petit DL 04-09-07 à 16:18

Citation :
Quant au terme général, je jète l'éponge


Le terme général m'intéresse.
J'ai essayé de m'y attaquer mais j'ai aussi jeté l'éponge. Le mieux que je puisse faire est de l'exprimer sous forme d'une somme (infinie ou finie).

En fait, je suis passé par le développement en série entière de l'exponentielle.
On a \Large{e^{u}=\Bigsum_{n=0}^{+\infty}\frac{u^n}{n!}

donc

\Large{f(x)=\Bigsum_{n=0}^{+\infty}\frac{1}{n!(1-x)^{n+1}}}

Ensuite, on sait que pour x proche de 0 (plus précisément pour |x|<1), on a :

\Large{(1-x)^{-n-1}=\Bigsum_{p=0}^{+\infty}\frac{(n+1)...(n+p)}{p!}x^{p}}


Ensuite, grâce au théorème de Fubini, on peut intervertir les deux sommes (j'avoue, je vais un peu vite ) :


\Large{f(x)=\Bigsum_{p=0}^{+\infty}\frac{a_p}{p!}x^p}

avec \Large{a_p=\Bigsum_{n=0}^{+\infty}\frac{(n+1)...(n+p)}{n!}}

Ainsi, f est développable en série entière au voisinage de 0 et pour tout entier naturel p,

\Large{f^{(p)}(0)=a_p}

une remarque pour essayer d'expliciter un plus cette somme :

si on pose \Large{g(x)=x^{p}e^x}, alors :

\Large{g(x)=\Bigsum_{n=0}^{+\infty}\frac{x^{n+p}}{n}}

donc :

\Large{g^{(p)}(x)=\Bigsum_{n=0}^{+\infty}\frac{(n+1)...(n+p)}{n!}x^{n}}


d'où :

\Large{a_p=g^{(p)}(1)}.

En dérivant g grâce à la formule de Leibniz, on a :

\Large{g^{(p)}(x)=\Bigsum_{k=0}^{p}C_{k}^{p}\(\frac{p!}{(p-k)!}x^{p-k}\)e^{x}}

d'où :

\Large{a_p=e(p!)^2\Bigsum_{k=0}^{p}\(\frac{1}{k!((p-k)!)^2}\)}

Bref, pas terrible.
J'ai donc utilisé l'arme ultime : mon ami Maple.
voici ce qu'il me propose :

Petit DL

Traduction : pas la peine de se casser la tête plus longtemps !

J'ai regardé dans l'aide de Maple. Ces fameuses fonctions de Kummer sont des solutions de certaines équations différentielles du second ordre mais ça s'arrête là. !

Kaiser

Posté par
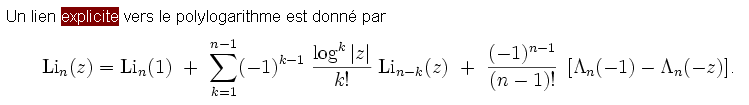
mikayaoure : Petit DL 04-09-07 à 16:25

bien, au moins, on pourra se pencher sur les fonctions de Kummer et les polylogarithmes

Posté par
kaiser Moderateurre : Petit DL 04-09-07 à 16:28

J'en trépigne d'impatience !

Kaiser

Posté par
mikayaoure : Petit DL 04-09-07 à 16:31



surtout quand on voit que wiki utilise le mot explicite dans la relation suivante donnée ici :

Petit DL

pour ma part, j'en frémis

Posté par
kaiser Moderateurre : Petit DL 04-09-07 à 16:37

eh ben, c'est joli tout ça !

Kaiser


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !