Inscription / Connexion Nouveau Sujet
Pivot de Gauss en fractions
Bonsoir,
x - y + z = 3 x - y + z = 3
-1/3x + 5/3y - z = 2 4/3y - 2/3z = 3
-1/2x + y - z = 1/4 -1/2z = 7/4
Je trouve ainsi :
z = -7/8
y = 29/16
x = 48/-43
Êtes-vous d'accords ? Merci
Merci beaucoup, j'ai rectifié.
Cependant je ne comprends pas le : x = 13/2
si je remplace : x - y + z = 3
x - 1 + (-5/2) = 3
x - (2/2 +(-5/2) = 3
x - (-3/2) = 3
x + (3/2) = 3
x = 3 / (3/2)
x = (3/1) * (2/3)
x = 6/3
...
Cependant je ne comprends pas le : x = 13/2
y = 1
z = -5/2
Vérification de la première équation :
x - y + z = 3
13/2 - 1 - 5/2 = 13/2 - 2/2 - 5/2 = (13 - 2 - 5)/2 = 6/2 = 3
Donc ça marche très bien...
si je remplace : x - y + z = 3
x - 1 + (-5/2) = 3
x - (2/2 +(-5/2) = 3
...
...
...
OK ?
Vu ?
Bon tu sais ce qu'il te reste à faire
 ...
...x - y + z = 3
x - 1 + (-5/2) = 3
x - (2/2 +(-5/2) = 3
...
Non je ne vois pas, je n'arrive pas à trouver 13/2 ..
Au secours !!
Non je ne vois pas, je n'arrive pas à trouver 13/2
x - (2/2 +(-5/2) = 3
Tu ne vois vraiment pas que tu as écris une grosse daube
 ?
?
Combien de parenthèses ouvrantes ?
Combien de parenthèses fermantes ?
J'ai une bonne adresse d'opticien si t'as des problèmes pour te relire.
Recommence proprement ton calcul.
Si vraiment tu as du mal : fais comme moi dans le post de 1h19.
Et si tu ne vois pas, je ne sais pas ce qu'on peut faire.
Je t'ai donné la bonne solution, avec le bon calcul.
Tu as donné un calcul faux et je t'ai dit ce qui clochait dedans.
Donc là il va falloir te prendre un peu en charge
 ...
...salut
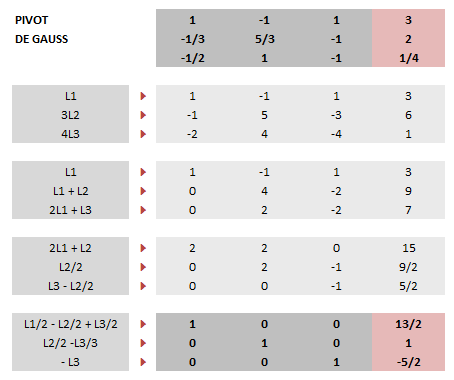
faut être bourrin pour calculer avec des fractions ...
x - y + z = 3
-x + 5y - 3z = 6
-x + 2y - 2z = 1/2
x - y + z = 3
4y - 2z = 9
y - z = 7/2
x - y + z = 3
y - z = -7/2
2z = -5
....
faut être bourrin pour calculer avec des fractions ...
Le problème n'est même pas là.
Dans la première étape du pivot j'ai justement viré toutes les fractions...
Mais même avec la solution livrée clé en main, Lauren n'arrive pas à voir que le système est vérifié : c'est la dessus qu'il dit être bloqué...
Bonjour,
Je sais que mon message est un peu hors-sujet, qu'on me pardonne.
La méthode du pivot de Gauss a été mise au point pour résoudre des systèmes avec de nombreuses équations, en tout cas, plus que 3 et surtout avec des valeurs réelles, puisque c'est une méthode de calcul numérique.
Or les exercices que je vois ont peu d'équations et des valeurs exactes.
Par ailleurs, l'un des éléments important de cette méthode est de classer les équations en fonction de la valeur des paramètres.
Je ne me souviens pas l'avoir vu évoqué dans une correction.
Je suis persuadé que cette méthode fait partie des programmes parce qu'elle est utilisée en informatique, là où on constate tout son intérêt.
La méthode du pivot de Gauss a été mise au point pour résoudre des systèmes avec de nombreuses équations, en tout cas, plus que 3 et surtout avec des valeurs réelles, puisque c'est une méthode de calcul numérique.
Or les exercices que je vois ont peu d'équations et des valeurs exactes.
Par ailleurs, l'un des éléments important de cette méthode est de classer les équations en fonction de la valeur des paramètres.
Je ne me souviens pas l'avoir vu évoqué dans une correction.
Bonjour Dlzlogic,
Il me semble en effet "qu'autrefois" on ne montrait pas le pivot de Gauss en taupe.
On procédait par substitutions ou par combinaisons linéaires (ce qui revient au même...).
Le pivot de Gauss était surtout vu (ultérieurement, en école d'ingénieur) comme méthode d'analyse numérique.
Aujourd'hui il semble qu'un "rapprochement" ait été fait entre ces différentes présentations.
Le pivot de Gauss a effectivement "vocation" à être utilisé pour des système numériques complexes et de grandes tailles, avec une aide informatique (programme ou simple tableur), totale ou partielle.
Mais rien n'empêche de l'utiliser également sur quelques équations avec des coefficients simples.
Outre le gain éventuel de temps (une fois qu'on maîtrise la méthode), on peut aussi établir un lien entre la manipulation classique d'équations, et une représentation plus adaptées à l'automatisation.
Lorsque le pivot n'est pas (complètement) automatisé, il peut garder quelques degrés de liberté.
Il n'est notamment pas indispensable de trier les équations selon leur paramètres.
Pour ma part, j'ai écrit une moulinette très simple sur tableur qui règle illico leur compte aux systèmes d'ordre 3 ou 4, et qui de surcroit propose des combinaisons linéaires plutôt simples, surtout lorsque les systèmes ont une bonne tête... ce qui est généralement le cas dans les exercices pédagogiques... A l'usage, c'est quand même bien pratique pour vérifier les exercices postés par les étudiants...

 3
3
 algèbre en post-bac
algèbre en post-bac