Inscription / Connexion Nouveau Sujet
Point d'accumulation/isolé
Bonsoir,
Je sèche complètement sur ces notions de topologie. Je suis dans un cours de MPSI sur la continuité des fonctions (notion hors programme mais compléments de topologie de l'auteur). J'ai vraiment du mal en topologie donc ça serait gentil d'y aller doucement.
J'ai appris les définitions de voisinage, point adhérent, point intérieur, frontière. Je pense avoir compris.
On dit qu'un élément x d'un espace métrique est un point d'accumulation à une partie A de E lorsque pour tout voisinage V de x :
On dit qu'un élément x est un point isolé de A s'il existe un voisinage V de x tel que :
1/ Soit
Décrire les points d'accumulation et les points isolés s'ils existent.
2/ Soit
2 est-il un point adhérent ? Un point isolé ? Un point d'accumulation ?
Quel est l'ensemble des points d'accumulation de A ?
Je serai preneur pour des indications 
Bonsoir,
En fait ces notions sont assez bien nommées et intuitives, tu peux voir les voisinages comme un "réticule" quand tu regardes un point.
Si un point est isolé alors si on regarde assez près on ne verra que lui.
Si un point est d'accumulation alors on aura beau faire il ne sera jamais seul.
Si tu as compris come tu dis tu peux voir tout seul (en faisant un dessin pour t'aider) ce qui se passe dans tes exemples.
Par exemple dans 2) quelle est l'intersection du voisinage avec
?
Est-ce que tu peux trouver un voisinage de 1 qui ne rencontre pas
etc...
Je pense ne pas avoir compris les notions de points isolés et d'accumulation vu que j'arrive pas à faire l'exo.
Je commence sur le cas 2. 2 est-il un point adhérent ?
2 est adhérent à A si et seulement si :
Prenons :
car 2 est contenu dans l'intervalle
Mais il faut le montrer pour tous les epsilon non ?
Bonjour Ramanujan.
Dans 2/, le point est un point de A, donc il est nécessairement adhérent à A puisque tout voisinage de 2 contient 2 (par définition), lequel est un point de A.
En revanche, ton post montre que 2 est isolé dans A puisque pour e = 1/2, tu as un voisinage de 2 (en l'occurrence [1,5 ; 2,5 ]) qui ne rencontre pas A.
Vu qu'il est isolé, il ne peut pas être point d'accumulation.
Donc 2 est un point adhérent et isolé.
Impossible de trouver un voisinage de A qui ne rencontre pas 1 car donc : 1 est un un point adhérent de A ?
2 est-il un point d'accumulation ?
Non car ça voudrait dire que tout voisinage de x rencontre A en un autre point que 2.
Pour
Donc 2 n'est pas un point d'accumulation.
Là où je me suis embrouillé je pense est que dans la définition de voisinage c'est alors qu'ici c'est "pour tout voisinage de x"
Maintenant je cherche les points d'accumulation de A 
Donc 2 est un point adhérent et isolé.
Tout-à-fait ...

Impossible de trouver un voisinage de A qui ne rencontre pas 1 car
Ici, tout dépend :
- si tu considères A comme un espace à lui tout seul, la question de savoir quelle est la nature de 1 n'a pas de sens puisque.
- si tu considères A comme une partie de
J'imagine que c'est de la seconde option qu'il s'agit ...

2 est-il un point d'accumulation ?
2 est un point isolé. Or un point ne peut être à la fois isolé et d'accumulation.
Toute partie d'un espace métrique peut être décomposée en une partition formée, d'une part de ses points d'accumulation et d'autre part, de ses points isolés. (Toute partie sans point isolé s'appelle un ensemble parfait.)
Partant, tu devrais pouvoir trouver les points d'accumulation de A
Complément :
- si tu considères A comme un espace à lui tout seul, la question de savoir quelle est la nature de 1 n'a pas de sens puisque
Merci beaucoup Jsvdb
Ici on considère l'espace métrique où :
A est une partie de E.
0 est un point d'accumulation de A car pour tout epsilon
0.5 est un point d'accumulation de A car pour tout epsilon
1 est un point d'accumulation de A car pour tout epsilon
Donc l'ensemble des points d'accumulation de A est
C'est juste ?
Pour l'ensemble :
Je dirais que 0 est point d'accumulation de A car :
On peut toujours trouver un il suffit de prendre un n assez grand.
Pour les points isolés de je n'y arrive pas

Je t'ai dit de faire un dessin !
Tu verras bien qu'entre il y a un trou où tu peux faire beaucoup de choses...
Merci Luzak je pense avoir trouvé grâce à votre indication.
Voici mon dessin qui montre que tout point de A est un point isolé de A.
Il suffit de prendre : et
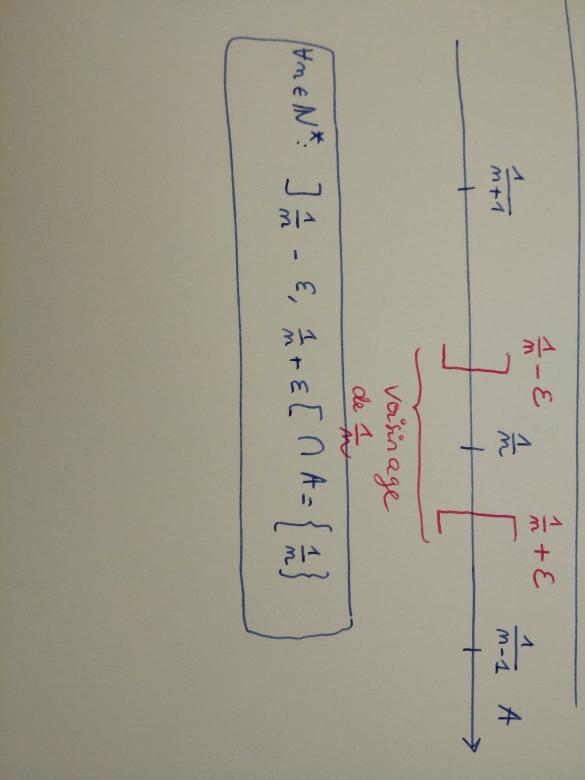
1 est un point d'accumulation de A car pour tout epsilon
Donc l'ensemble des points d'accumulation de A est
C'est juste ? NON

Un point d'accumulation appartient forcément au sous-ensemble que l'on considère.
Rappelle-toi, un sous-ensemble est formé de ses points d'accumulation et de ses points isolés (et c'est une partition).
Donc l'ensemble des points d'accumulation de
A contrario, et comme A est vu comme un sous-ensemble de
Vous êtes sûrs ?
0 est point d'accumulation de A et 1 aussi ...
J'ai juste appliqué la définition. Je comprends pas votre réponse.
Pour les points d'accumulations, j'ai relu la définition x doit appartenir à l'espace métrique pas forcément à A ....
Bonjour
pour jsvdb : on ne lui demande pas les points d'accumulation de A, mais les points d'accumulation à A ....
A peut être la réunion de ses points d'accumulation et de ses points isolés, il n'empêche qu'il peut exister des points d'accumulation à A ailleurs que dans A
ok ok ... j'ai bien saisi maintenant ... 
On demandait donc les points adhérents à
.
Dans ce cas, oui, 0 et 1 sont bien de la partie, et pas 2 ...
Bonjour lafol !
Je ne saisis pas l'intérêt de tes "discriminations" !
est point d'accumulation de( oui, de)
si tout voisinage épointé de
rencontre
.
Je ne vois pas l'intérêt de savoir si ou
.
....................................
"Point d'accumulation à" : jamais vu cette notion et en plus, question langue, c'est vraiment limite.
C'est plus facile avec "adhérent" puisque "adhérent à" ferait plaisir à tout grammairien.
Mais on dit bien dans "l'adhérence de
" sans qu'il y ait
.
Il faudrait inventer le vocable "accumulé à" ?
Le mieux est de ce passer du mot " accumulation " et de définir un ensemble .
E étant un topologique et A une de ses parties on définit Acc(A) comme l'ensemble formé des x de E tel que tout voisinage de x rencontre A \ {x} .
Je crois que Choquet avait adopté la notation A ' au lieu de Acc(A) et l'appelait l'ensemble dérivé de A .
@luzak : il n'y a pas de discriminations dans les propos de lafol, c'est simplement moi, qui, une fois de plus, ai encore compliqué les choses en voulant faire une distinction stupido-débile entre l'ensemble A pris comme espace et l'ensemble A pris comme sous-espace. Et évidemment, je me suis pris les pieds dans le tapis.
@etniopal : tout-à-fait d'accord 
je reprenais juste les termes de la définition citée par Ramanujan :
On dit qu'un élément x d'un espace métrique
On dit qu'un élément x est un point isolé de A s'il existe un voisinage V de x tel que :
qui lèvent l'ambigüité sur le fait qu'un tel point d'accumulation doive ou non appartenir à A...


 topologie en post-bac
topologie en post-bac