Inscription / Connexion Nouveau Sujet
Polygône à n cotés!
Bonjour j'ai quelques problèmes à effectuer cet exercice:
Les poitns A, B et C sont tois sommets consécutifs d'un polygone régulier de centr O et ayant N cotés, avec N est supérieur ou égal à 3.
Question: Exprimer en fonction de n la mesure de l'angle ABC
J'ai essayé de mon coté de calculer l'angle au centre A0C : 2x360/N = 720/N
Mais je bloque au moment de prouver que l'angle au inscrit ABC mesure le double de AOC (d'après le théorème de l'angle inscrit)
Oui merci mais quel est le calcul?
AOC = 2 x 360 / N
AOC = 720 / N
Donc AOB = (360 - 720 / N) / 2
Juste? Et quel est le résultat je bloque..
javascript:void(0)
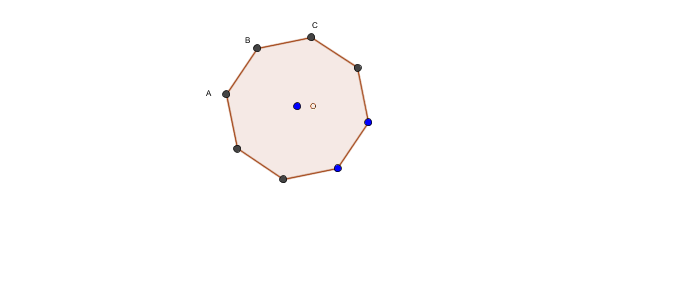
J'ai dessiné un octogone.( N=8 côtés)
Chaque arc vaut 360/8=45°
L'angle inscrit ABC est égal à la moitié de l'angle au Centre COA
Et l'angle COA intercepte l'arc AC ( qui est "composé" de 6 petits arcs de 45°) qui vaut 270°
Donc l'angle inscrit ABC= (6 x45°)/2= 135°
Exprimer en fonction de n la mesure de l'angle ABC
ABC= [(360/N)x (N-2)/2]
Bonjour à vous deux
Une autre façon :
L'angle AOB=360°/N
le polygone étant régulier, les triangles composant ce dernier, tels que AOB sont tous isocèles en O et les 2 autres angles de ce triangle sont égaux et valent (180°-(360°/N))/2 et l'angle ABC vaut 2 fois cet angle
soit 180°-(360°/N)
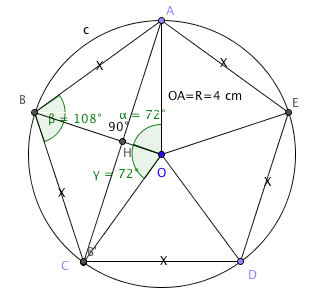
exemple pour un pentagone régulier :
l'angle AOB vaut 360°/5=72°
OÂB=OBA=(180°-(360°/5))/2=(180°-72°)/2=108°/2=54°
et ABC=2*54=108°
illustration prise sur un autre topic
bonjour mijo,
ABC= [(360/N)x (N-2)/2]
dans ton exemple N=5
(360/N)x (N-2)/2] - > (360/5) x (5-2)/2 = 108°
Mais force est de reconnaître que ta démonstration est complète.
bonne soirée
Bonsoir kenavo27
Je n'ai pas dit que ce que tu as écrit n'est pas bien, ton application le prouve, j'ai indiqué simplement une variante.


