Inscription / Connexion Nouveau Sujet
Position relative
Bonjour Madame et Messieurs
On vient de commencé le chapitre sur la Géométrie dans l'espace et je n arrive pas a comprendre les leçon et je fait des exercice pour comprendre . Mais j'ai vue des vidéo pour comprendre c'est quoi un plan , mais j arrive pas à comprendre .
Voici l'exercice :
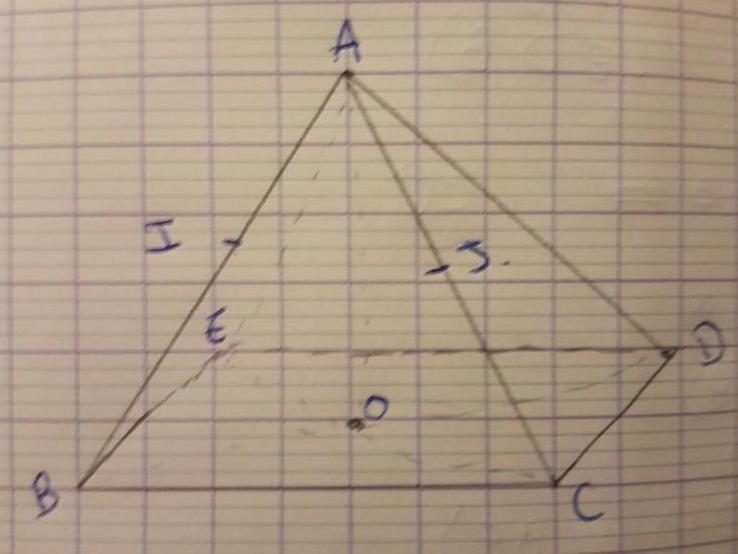
ABCDE est une pyramide telle que BCDE soit un parallélogramme de centre O et de hauteur AO.
I est le milieu du segment [AB]. J est le milieu du segment [AC]
1. Représenter cette pyramide en perspective cavalière et y placer les points I et J.
2. Préciser, en justifiant, les intersections:
a. des plans (ABC) et (ACD);
b. des plans (ABD) et (AEC);
c. de la droite (AO) et du plan (BED);
d. des droites (DI) et (AO).
3. Démontrer que la droite () et le plan (BCD) sont parallèles.
4. Démontrer que la droite (1J) et la droite (ED) sont parallèles.
5. En déduire l'intersection des plans (ABC) et (ElD).
Ps: J'ai fait la 1 .
salut
qu'ont en commun de façon évidente les plans (ABC) et (ACD) ? conclusion ?
qu'ont en commun de façon évidente les plans (ABD) et (AEC) ?
que nous faut-il ?
PS : une figure serait la bienvenue ...
ok merci pour l'image ... dommage qu'elle ne soit pas dans le bon sens ...
[b]Mais j'ai vue des vidéo pour comprendre c'est quoi un plan , mais j arrive pas à comprendre .

Ça veut dire que dans l'espace il y a la pyramide et dans la pyramide il y a des plan et dans les plan il y a des point à l'infini . Par exemple , est ce que le plan (ACE) existe . Je pense que oui .
a. des plans (ABC) et (ACD);
Est ce que on peut dire que dans le plan (ABC) et (ACD) . L'intersection c'est le point C car ces sur le point C et le plan (ABC) et (ACD) sont sécantes .
ben oui !!
que signifie la notation (ACE) ?
est-ce que la droite (AC) existe ?
que signifie la notation (AC) ?
Je reformule : B (ACD)
(ACD)
C  (ABC) et (ACD)
(ABC) et (ACD)
A (ABC) et (ACD)
(ABC) et (ACD)
L'intersection de (ABC) et (ACD) c'est la droite (AC) .
b. des plans (ABD) et (AEC);
A (ABD) et (AEC)
(ABD) et (AEC)
O (BD) et (EC)
(BD) et (EC)
c'est à dire O ( ABD) et (AEC)
( ABD) et (AEC)
L'intersection de (ABD) et (AEC) c'est la droite (AO)
c. de la droite (AO) et du plan (BED);
Je n ai pas compris cette question . Est ce que vous pouvez m'éclaire si vous plait .
C'est quoi un plan dans l'espace ?
L'espace, c'est quoi : ta chambre représente l'espace. Ou en regardant par la fenêtre, l'espace, c'est tout l'air que tu vois autour de toi.
Un plan dans l'espace : ta table est un plan, Chaque mur est un plan, une feuille de papier est un plan.
En fait, tout ça ce sont des morceaux de plans. Un plan , ce serait une très grande feuille de papier. Si grande que tu ne vois pas les bords.
Mais si on revient aux murs, le plancher, et 2 murs, ça donne 3 plans. Et ces plans peuvent représenter un repère, un repère orthogonal, ou même orthonormé.
Le plancher et le plafond sont 2 plans parallèles.
Etc etc.
Bonjour,
Je réponds en l'absence des intervenants d'hier.
Un plan n'est pas constitué de 3 points mais d'une infinité de points.
De même une droite n'est pas constituée de 2 points mais d'une infinité de points.
Une droite peut être définie par 2 poins distincts.
Un plan peut être défini par 3 points non alignés.
Et si tu lisais un cours sur la géométrie dans l'espace ?
Tu n'as pas un cours ou un livre ?
Je vais voir ce qu'il y a sur l'île.
Tes réponses sont bonnes ; mais il manque une justification :
Après avoir trouvé deux points communs distincts aux deux plans, il faut dire pourquoi les plans ne sont pas confondus.
Pour ça, il suffit de citer un point qui est dans l'un et pas dans l'autre.
Merci Madame pour cette leçon !
b)
b. des plans (ABD) et (AEC);
A
 (ABD) et (AEC)
(ABD) et (AEC)
O
 (BD) et (EC)
(BD) et (EC)
c'est à dire O
 ( ABD) et (AEC)
( ABD) et (AEC)
L'intersection de (ABD) et (AEC) c'est la droite (AO)
C
 (ABD)
(ABD)
B
 (AEC)
(AEC)
Pour la c) j 'arrive pas a comprendre car il y a droite et plan dans la même question .
Lire
3.Les droites et les plans :
Ou chercher "position relative de droites et plans".
Oui : L'intersection c'est le point O .
Et quand tu rédiges, précise : l'intersection de ... et de ... est le point C.
Une remarque sur l'intersection droite plan quand la droite n'est pas parallèle au plan :
Je n'aime pas l'expression "la droite coupe le plan".
Je préfère "le plan coupe la droite".
Ou, mais peu utilisé : "la droite perce le plan".
salutSylvieg : tu peux poursuivre car j'ai des copies à corriger et un BTS blanc à préparer !!
je passes de temps en temps comme ça mais foq est entre de bonnes mains donc n'hésite pas !!
au passage : malou aurait-elle bu un coup de trop avec tous ces anniversaires qui s'enchainent ? (voir image à 19h15 et son édit) 
étonnant : je reviens, je repars, je reviens et elle est toujours tournée !! (revenir = changer de page et y revenir)
je viens de faire un ctrl F5 et là oui maintenant elle est dans le bon sens

Est ce que c'est ça ?
3. Démontrer que la droite (IJ) et le plan (BCD) sont parallèles.
(IJ) // (BC) alors la droite (IJ) et le plan (BCD) sont parallèles .
4. Démontrer que la droite (IJ) et la droite (ED) sont parallèles.
(IJ)//(BC) et (BC)//(ED) . Alors la droite (IJ) et la droite (ED) sont parallèles.



 (DI)
(DI)
