Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Licence Maths 1e ann AnalyseTopics traitant de analyse [tout]Lister tous les topics de mathématiques
Niveau Licence Maths 1e ann
Partager :

Préparation au partiel - Maths L1 AES

Posté par
SAMYEL06 16-06-14 à 14:59

Bonjour,

Certains me connaissent içi car j'ai relativement souvent demandé de l'aide pour comprendre les maths

Je suis aujourd'hui à J-3 avant le grand partiel de ma vie, celui ou je devrais avoir un 15 pour valider la matière, et l'année !

Je vais donc passer ces 3 jours à faire des exercices de maths de niveau L1 AES afin d'espérer réussir le partiel de Jeudi, et je vous demande humblement votre aide durant ces 3 intenses journées qui se profilent.

Je commence dès maintenant avec un exercice complet, merci de m'indiquer les erreurs faites afin que je puisse m'améliorer

-----------------------------------------------------------------------------------------------------------------
Exercice 3 :

Soit f la fonction qui a (x,y) associe f(x,y) = x^4 - 4xy^3 + y^4

1) Calculer f(1;-1)
2) \partial f/\partial x et \partial f/\partial y de (1;-1)
3) Equation du plan tangeant au point (1;-1)
4) Déterminer les points critiques
5) Déterminer le Hessien au point (0,0), que peut on en dire ?
-----------------------------------------------------------------------------------------------------------------

1) Calculer f(1;-1)

f(x,y) = x^4 - 4xy^3 + y^4 \\ f(1,-1) = (1)^4 - 4(1)(-1)^3 + (-1)^4 \\ f(1,-1) = 1 - 4(-1) + 1 \\ f(1,-1) = 6

2) \partial f/\partial x et \partial f/\partial y de (1;-1)

\partial f/\partial x = 4x^3 - 12xy^2 \\ \partial f/\partial x (1,-1) = 4(1)^3 - 12(1)(-1)^2 \\ \partial f/\partial x (1,-1) = 4 - 12 \\ \partial f/\partial x (1,-1) = -8 \\ \\ \partial f/\partial y = -12xy^2 + 4y^3 \\ \partial f/\partial y (1,-1) = -12(1)(-1)^2 + 4(-1)^3 \\ \partial f/\partial y (1,-1) = -12 -4 \\ \partial f/\partial y (1,-1) = -16

3) Equation au plan tangeant (1,-1)

z - Z = \partial f/\partial x (1,-1) * (x - X) + \partial f/\partial y (1,-1) * (y - Y)

Z = 6 \\ \partial f/\partial x (1,-1) = -8 \\ \partial f/\partial y (1,-1) = -16 \\ X = 1 \\ Y = -1 \\ \\ z - 6 = -8(x - 1) + (-16)(y -(-1)) \\ z - 6 = -8x + 8 -16y -16 \\ z = -8x - 16y - 16 + 8 + 6 \\ z = -8x -16y -2

4) Déterminer les points critiques
4x^3 - 12xy^2 = 0 \\ -12xy^2 + 4y^3 = 0

a) 4x^3 - 12xy^2 ==> 4x((1)^3 - 3y^2) ==> x = 0
b) -12xy^2 + 4y^3 = 0 ==> 4y(-3x^2 + 1^3) ==> y = 0

Le point (0;0) est donc un point critique.

5) Déterminer le Hessien au point (0,0), que peut on en dire ?
\partial f/\partial x = 4x^3 - 12xy^2 \\ \partial f/\partial y = -12xy^2 + 4y^3 \\ \\ \partial^2 f/\partial x^2 = 12x^2 - 24xy \\ \partial^2 f/\partial y^2 = -24xy + 12y^2 \\ \\ \partial^2 f/\partial x\partial y = \\ \partial^2 f/\partial y\partial x =

Je bute là, je n'arrive pas à me souvenir comment on fais les deux derniers... :/ je sais je crois que c'est la dérivée de x dans y, et de y dans x, mais je ne sais plus comment proceder et je crois avoir fait faux ^^

Merci de bien vouloir m'aider, le temps m'est compté :/

Merci !

Posté par
Camélia Correcteurre : Préparation au partiel - Maths L1 AES 16-06-14 à 15:03

Bonjour

\dfrac{\partial f}{\partial x} est fausse.

\dfrac{\partial^2f}{\partial x\partial y}f=\dfrac{\partial}{\partial x}\left(\partial f}{\partial y}

Posté par
Camélia Correcteurre : Préparation au partiel - Maths L1 AES 16-06-14 à 15:06

\dfrac{\partial^2f}{\partial x\partial y}=\dfrac{\partial}{\partial x}\left( \dfrac{\partial f}{\partial y} \right)

Posté par
SAMYEL06re : Préparation au partiel - Maths L1 AES 16-06-14 à 15:15

Merci camélia,

Je pars de f(x,y) = x^4 - 4xy^3 + y^4
\partial f/\partial x = 4x^3 - 4y^3

Est-ce cela ? Parce que -4xy^3 = -4x * (y)^3 ? Et du coup -4x ne laisse que -4 ?

Merci !

(J'attends de savoir si c'est bien l'erreur que j'ai faite pour ensuite tout reprendre ^^")

Posté par
Camélia Correcteurre : Préparation au partiel - Maths L1 AES 16-06-14 à 15:21

Oui, c'est ça.

Posté par
SAMYEL06re : Préparation au partiel - Maths L1 AES 16-06-14 à 16:02

D'accord, compris

Donc je repars de zéro :

1) Calculer f(1,-1)

f(x,y) = x^4 - 4xy^3 + y^4 \\ f(1,-1) = 1^4 - 4(-1)(-1)^3 + (-1)^4 \\ f(1,-1) = 1 - 4(-1) + 1 \\ f(1,-1) = 6

2)
\partial f/\partial x = 4x^3 - 4y^3 \\ \partial f/\partial y = -12xy^2 + 4y^3

==>

\partial f/\partial x (1,-1) = 4(1)^3 - 4(-1)^3 = 4 - (-4) = 8 \\ \partial f/\partial y (1,-1) = -12(1)(-1)^2 + 4(-1)^3 = -12 + -4 = -16 \\

3)

z - 6 = 8(x - 1) + (-16)(y - (-1)) \\ z - 6 = 8x - 8 -16y -8 \\ z - 6 = 8x - 16y -8 - 8 \\ z = 8x - 16y -16 + 6 \\ z = 8x - 16y -10

4)
4x^3 - 4y^3 = 0 \\ -12xy^2 + 4y^3 = 0

a) 4(x^3 - y^3) = 0 ==> x = 0 et y = 0 ou x = -1 et y = -1
b) 4(-3xy^2 + y^3) = 0 ==> x = 0 et y = 0

Les points critiques sont (0,0) et (-1,-1)

5) Déterminer le hessien en (0,0)

On calcule d'abord les dérivées secondes :

\partial^2 f/\partial x^2  (0,0)= 12x^2 \\ \partial^2 f/\partial y^2 (0,0) = -24xy + 12y^2

Puis les dérivées de y dans x et x dans y :

\partial^2 f/\partial y\partial x (0,0) = -12y^2 \\ \partial^2 f/\partial x\partial y (0,0) = -12y^2

Enfin on établis la hessienne de (0,0) en calculant d'abord :

\partial^2 f/\partial x^2 (0,0)= 0 \\ \partial^2 f/\partial y^2 (0,0) = 0 \\ \\ \partial^2 f/\partial y\partial x (0,0) = 0 \\ \partial^2 f/\partial x\partial y (0,0) = 0

Donc
H(0,0) = 0 0
             0 0

Je ne sais plus comment le faire bien (la commande ^^")

Et que puis-je en dire ? Bien, le fait que ce soit aux points (0,0) rends les toutes les variables nulles, et donc la hessienne également, ce qui confirme que le point (0,0) est nul, et donc critique.

-------------

En espérant avoir mieux fait cette fois car ce n'est pas évident.. j'ai perdu la mécanique que j'avais apprise :/

Merci encore de m'aider !

Posté par
SAMYEL06re : Préparation au partiel - Maths L1 AES 16-06-14 à 16:05

PS : Je n'aurai pas du mettre les (0,0) dans toute l'explication du début du 5), désolé...

C'est les dérivées secondes de (x,y) et les dérivées de x dans y et de y dans x de (x,y), et non de (0,0), je n'aurai donc rien du mettre avant "Enfin, on calcule la hessienne de (0,0)...".

^^"

Posté par
SAMYEL06re : Préparation au partiel - Maths L1 AES 16-06-14 à 16:08

PS 2 : Erreur de signe au début c'est f(1,-1) = 1^4 - 4(1)(-1)^3 + (-1)^4

Posté par
Camélia Correcteurre : Préparation au partiel - Maths L1 AES 16-06-14 à 16:09

1) et 2) et 3) OK.

4) pas d'accord avec les points critiques.

Posté par
SAMYEL06re : Préparation au partiel - Maths L1 AES 16-06-14 à 16:17

C'est déjà ça pour le 1, 2 et 3 ! Ouf !

Pour le 4)

4(x^3 - y^3) ==> Si x = -1 et y = -1 alors 4((-1)^3 - (-1)^3) donc 4(-1 - (-1)) donc -4 - (-4) donc -4 + 4 = 0 , non ?

Et pour le (0,0) c'est évident je pense que c'est un point critique puisqu'il est toujours nul

Merci ^^"

Posté par
Camélia Correcteurre : Préparation au partiel - Maths L1 AES 16-06-14 à 16:24

Oui, mais pourquoi tu prends -1? Et ton -1 annule l'autre dérivée? C'est faux que (0,0) soit toujours critique, mais il se trouve que ici c'est vrai.

Rappel: x^3-y^3=(x-y)(x^2+xy+y^2)

Posté par
SAMYEL06re : Préparation au partiel - Maths L1 AES 16-06-14 à 16:30

Ah oui, ça n'annule pas l'autre dérivée.. tu as raison ! J'avais complètement oublié qu'ils n'étaient pas isolés mais que les points devaient annuler les deux dérivées et non une seule !

Pour ce qui est des identités remarquables, je suis totalement à la ramasse .. je n'y arrive pas :/ je me contente de factoriser (diviser les nombres dans la parenthèse par une division commune et la mettre en facteur) car sinon je n'y arrive pas trop :/

Pour ce qui est du 4 ==> Compris ! Et vu la difficulté de la seconde dérivée (b), il n'y a surement que (0,0) de compatible :/

Pour ce qui est du 5), est-il juste ? (ou partiellement) ?

Merci Camélia !

Posté par
Camélia Correcteurre : Préparation au partiel - Maths L1 AES 16-06-14 à 16:35

Non, il y a d'autres points critiques.

C'est vrai que la hessienne est nulle en (0,0)... et tout ce qu'on peut dire à priori c'est qu'on ne peut pas conclure si le point (0,0) est un extremum local. En fait il ne l'est pas!

Posté par
SAMYEL06re : Préparation au partiel - Maths L1 AES 16-06-14 à 17:23

Ah ?? Comment trouves tu les autres ? Car c'est quand même vachement compliqué non ?

Penses tu que je puisse avoir quelques points en trouvant (0,0)? :/

Posté par
Camélia Correcteurre : Préparation au partiel - Maths L1 AES 16-06-14 à 17:34

C'est pas si compliqué que ça!

Il faut résoudre

4(x^3-y^3)=4(x-y)(x^2+xy+y^2)=0

qui donne juste x=y et AUSSI

0=-12xy^2+4y^3=4y^2(-3x+y) qui donne y=3x ou y=0

Et... en effet il n'y en a pas d'autres, puisque y=3x=x n'est possible que pour x=y=0

Désolée, je l'avais fait de tête... mais tant qu'on n'a pas écrit tout ça, on n'a pas fini l'exo!

Posté par
SAMYEL06re : Préparation au partiel - Maths L1 AES 16-06-14 à 22:04

Pas si compliqué que ça ? Un peu quand même !

Je ne comprends pas trop comment tu obtiens 4(x - y)(x^2 + xy + y^2)

Celà dit, ce n'est pas très important, je vise le 15 pas le 20 donc j'ai le droit de ne pas comprendre certains points (et tant que je trouve au moins un point critique, ca me fais des points)..

Mais bon, si je pouvais comprendre ça, ce serait quand meme mieux ^^" !

Sinon la Hessienne est bonne ? (avec les dérivées secondes et les dérivées partielles de x et y dans x et y) ?

Merci

Posté par
Camélia Correcteurre : Préparation au partiel - Maths L1 AES 17-06-14 à 13:59

Oui, la hessienne est bonne.

Mais vraiment tu devrais connaitre les identités remarquables...

Posté par
SAMYEL06re : Préparation au partiel - Maths L1 AES 17-06-14 à 14:04

Suite à un problème je ne pourrais faire d'exercices que ce soir. Pour ce qui est des identités remarquables je sais que je ne suis pas bon mais il est un peu tard maintenant sachant que le partiel est le 19 :/

Ce soir je reverrais l'exercice d'hier et j'essaierai d'en faire un.

Demain je posterais un exercice sur la partie stats afin de revoir cette partie également.

En espérant avoir le temps de tout revoir !!

Merci encore Camélia !!

Posté par
Camélia Correcteurre : Préparation au partiel - Maths L1 AES 17-06-14 à 14:09

C'est toi qui vois... Pour les stats, c'est sans moi! Bon courage!

Posté par
lafol Moderateurre : Préparation au partiel - Maths L1 AES 17-06-14 à 16:53

Bonsoir
pour les identités remarquables, si les apprendre te parait insurmontable d'ici le 19, tu peux aussi voir que le polynôme en x x^3 - y^3 s'annule si on remplace x par y : ça signifie qu'on peut mettre (x-y) en facteur

après soit tu poses la division de x^3 - y^3 par x - y comme on le faisait à l'école primaire, en laissant de la place entre x^3 et y^3 pour avoir la place d'écrire les x² et les x dans les soustractions, comme ci dessous (je n'ai pas mis la dernière soustraction ni le dernier reste, 0)
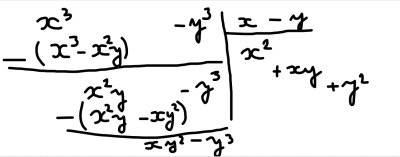
Préparation au partiel - Maths L1 AES

soit tu travailles par coeff indéterminés : x^3 - y^3 = (x-y)(x^2 + ...x + y^2) (ceux des extrémités sont imposés pour avoir les bons cubes)
en redéveloppant ça tu vois qu'il faut mettre y à la place des pointillés.


Rechercher
Menu
Espace membre
36 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1722 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !