Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Maths sup AnalyseTopics traitant de analyse [tout]Lister tous les topics de mathématiques
Niveau Maths sup
Partager :

Primitive...

Posté par bahamut (invité) 16-08-05 à 14:54

  
      Bonjour tout le monde! J'ai un petit problème avec cette primitive à calculer:
  
    \int_0^{1}Arctan(3x/(1-2x²))dx

      Merci de votre aide...

Posté par
Nightmarere : Primitive... 16-08-05 à 15:13

Bonjour

Le plus gros probléme ici est la fonction trigonométrique.
On sait par contre que Arctan'(x)=1/(1+x²)

Donc que dirais-tu d'une intégration par partie en primitivant 1 et en dérivant Arctan(3x/(1-2x²)) ?

A toi d'essayer

Jord

Posté par bahamut (invité)re : Primitive... 16-08-05 à 15:57



   Oui j'avais déja essayé mais le n'ai pas l'impression que ca arrange de trop puisque qu'aprés on a la primitive de  \frac{4x^5-4x^3+x}{4x^4+5x^2+1}  à calculer... je vais essayer de la calculer...

Posté par
Nightmarere : Primitive... 16-08-05 à 16:07

Tu as du te tromper car je trouve au numérateur :
3$\rm 6x^{3}+3x

Et ce n'est pas dur à primitiver (au passage, tu n'as plus le droit à l'erreur en post bac, on ne dit pas la primitive mais les primitives), il suffit de décomposer en élément simple. Par chance le dénominateur est bicarré. Pour le factoriser pose X=x²


jord

Posté par
Nicolas_75 Correcteurre : Primitive... 16-08-05 à 16:35

Je dirais qu'avant toute chose, il faut regarder le domaine de définition de l'intégrale. Ici pour x=1/V2, ce n'est pas très joli. Il doit y avoir 2, 3 choses à justifier, non ?

Posté par
J-P Posteur d'énigmesre : Primitive... 16-08-05 à 16:37

Es-tu sûr Nightmare ?

J'ai fait la dérivée de tête sans rien écrire (et donc j'ai pu me planter) et je trouve comme bahamut.


Posté par
Nightmarere : Primitive... 16-08-05 à 16:40

Ma calculette est sur J-P Enfin bon aprés elle peut avoir un gros probléme de conception mais je ne pense pas

Posté par
Nightmarere : Primitive... 16-08-05 à 16:42

Oui Nicolas_75, mais ça je pense que bahamut peut le faire seul et n'a pas besoin de nous (sinon il y a un probléme )


jord

Posté par
Nicolas_75 Correcteurre : Primitive... 16-08-05 à 16:56

Nightmare, je pense en effet que bahamut peut le faire seul. Néanmoins, comme il/elle semblait avoir des souci avec une intégrale "classique", je me disais qu'il avait pu "ne pas voir" qu'elle cachait une singularité. Ce sont des choses qui peuvent arriver. Comme personne dans le fil n'a relevé ce point, je préfèrais le faire par précaution.

Posté par
J-P Posteur d'énigmesre : Primitive... 16-08-05 à 17:01

C'est effectivement moins sujet à l'erreur en écrivant.

f(x) = arctg(3x/(1-2x²))

f '(x) = [1/(1 + 9x²/(1-2x²)²)]*[(3-6x²+12x² )/(1-2x²)²]

f '(x) = (6x²+3)/((1-2x²)²+9x²)

f '(x) = (6x²+3)/(4x^4 + 5x²+1)

Et on est donc bien amené à chercher une primitive de  (6x³+3x)/(4x^4 + 5x²+1).
-----


Posté par
J-P Posteur d'énigmesre : Primitive... 16-08-05 à 17:02

Zut encore une bêtise, tant pis.

Posté par
Nightmarere : Primitive... 16-08-05 à 17:02

Oui c'est sur Nicolas je comprend ton point de vue

J-P tu m'impressionne tout de même d'avoir essayé de faire ce calcul de tête


jord

Posté par
J-P Posteur d'énigmesre : Primitive... 16-08-05 à 17:05

C'était du temps où j'étais jeune que je pouvais faire cela, mais depuis j'ai perdu une volée de neurones et donc je me plante.


Posté par bahamut (invité)re : Primitive... 16-08-05 à 17:16

     Merci

Posté par
Nightmarere : Primitive... 16-08-05 à 17:18

Pas de probléme


Jord

Posté par
elhor_abdelali Correcteurre : Primitive... 17-08-05 à 19:58

Bonjour à tous;
la fonction f:x\to arctan(\frac{3x}{1-2x^2}) est continue sur [0,\frac{\sqrt{2}}{2}[\cup]\frac{\sqrt{2}}{2},1] avec \{{\lim_{{\frac{\sqrt{2}}{2}}^{-}}f=\frac{\pi}{2}\\ \lim_{{\frac{\sqrt{2}}{2}}^{+}}f=-\frac{\pi}{2} elle est donc prolongeable en une fonction continue par morceaux sur [0,1] et par conséquent intégrable sur ce dernier.
Comme l'a vu Nightmare (Modérateur),la dérivée de f a une expression continue sur [0,1]:f'(x)=\frac{6x^2+3}{4x^4+5x^2+1} mais attention cela ne veut pas dire que f est dérivable sur [0,1](puisqu'elle n'y est pas continue)mais seulement que les 2 pentes à gauche est à droite de \frac{\sqrt{2}}{2} sont égales ( f' est elle-mm continue par morceaux sur [0,1] )
on conclue de ces remarques que l'on peut faire une intégration par parties sur [0,1] sans séparer en \int_{0}^{\frac{\sqrt{2}}{2}} et \int_{\frac{\sqrt{2}}{2}}^{1} allons-y:
avec \{{g'(x)=1\\f(x)=arctan(\frac{3x}{1-2x^2}) on a \{{g(x)=x\\f'(x)=\frac{6x^2+3}{4x^4+5x^2+1} d'où:
\int_{0}^{1}f(x)dx=-arctan(3)+\int_{0}^{1}\frac{6x^3+3x}{4x^4+5x^2+1}dx=-arctan(3)+\int_{0}^{1}\frac{6x^3+3x}{(x^2+1)(4x^2+1)}dx une petite décomposition en éléments simples donne que:
\frac{6x^3+3x}{(4x^2+1)(x^2+1)}=\frac{x}{x^2+1}+\frac{2x}{4x^2+1} et donc que:
3$\red\int_{0}^{1}arctan(\frac{3x}{1-2x^2})=\frac{1}{2}ln(2)+\frac{1}{4}ln(5)-arctan(3)
Sauf erreur bien entendu

Posté par jmix90 (invité)re : Primitive... 17-08-05 à 20:26

Car il t'arrive de faire des erreurs ? hi hi hi !

Posté par
J-P Posteur d'énigmesre : Primitive... 17-08-05 à 20:27

Sans calculs:

(1/2)ln(x) + (1/4)ln(5) - arctg(3) = -0,5 (environ)

Cela me fait dire que la solution de elhor_abdelali n'est pas correcte.
-----
Il suffit pour s'en convaincre de tracer f(x)=arctg(3x/(1-2x²)), l'aire en haut de l'axe des abscisses est > que  l'aire en bas de l'axe des abscisses.

La solution ne peut -etre que positive.

A la louche, les aires en bleu se neutralisent et l'aire restante est environ 1*0,4 /2 = 0,2

Les solutions proches de 0,2 ont une chance d'être correctes, pas les autres.
-----
Sauf si j'ai dit des bêtises.  



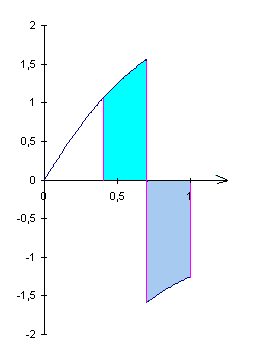
Primitive...

Posté par
J-P Posteur d'énigmesre : Primitive... 17-08-05 à 21:56

On trouve une primive telle que:

F(x) = x.artg(\frac{3x}{1-2x^2}) - \frac{1}{2}ln(x^2+1) - \frac{1}{4}ln(4x^2+1)

L'integrale = [F(x)]_0^{\frac{1}{\sqrt{2}}-} + [F(x)]_{\frac{1}{\sqrt{2}}+}^1

L'integrale = [x.artg(\frac{3x}{1-2x^2})]_0^{\frac{1}{\sqrt{2}}-} + [x.artg(\frac{3x}{1-2x^2})]_{\frac{1}{\sqrt{2}}+}^1 - [\frac{1}{2}ln(x^2+1) + \frac{1}{4}ln(4x^2+1)]_0^1

L'integrale = [\frac{1}{\sqrt{2}}.\frac{\pi}{2}] + [\frac{1}{\sqrt{2}}.\frac{\pi}{2}] - arctg(3) - [\frac{1}{2}ln(2) + \frac{1}{4}ln(5)]

L'integrale = \frac{\pi}{\sqrt{2}} - arctg(3) - \frac{1}{2}ln(2) - \frac{1}{4}ln(5)]

Ce qui est environ = à 0,2234...
Pas très loin des 0,2 estimé dans ma réponse précédente, c'est déjà cela.
-----
Sauf distraction.  




Posté par
elhor_abdelali Correcteurre : Primitive... 17-08-05 à 23:00

Eh oui jmix,tout le monde peut se tromper,ici il fallait justement séparer les 2 intégrales car x\to xarctan(\frac{3x}{1-2x^2})-\frac{1}{2}ln(x^2+1)-\frac{1}{4}ln(4x^2+1) est une primitive de x\to arctan(\frac{3x}{1-2x^2}) sur chaqu'un des intervalles [0,\frac{\sqrt{2}}{2}] et [\frac{\sqrt{2}}{2},1] mais pas sur [0,1].
Bien vu J-P (Correcteur)

Posté par jmix90 (invité)re : Primitive... 17-08-05 à 23:10

Bonjour,

C'est pas grave elhor tu reste un héro pour moi

Cependant.. dans quel cas peut on prolonger par continuité comme tu l'as fait ( à tort !)? Seulement quand les valeurs atteintes aux bornes sont les mêmes ?

Amicalement

Posté par
elhor_abdelali Correcteurre : Primitive... 18-08-05 à 02:44

Absolument jmix,ici par exemple on pouvait considérer la fonction:
g(x)=\{{arctg(\frac{3x}{1-2x^2}) , 0\le x\le\frac{\sqrt{2}}{2}\\arctg(\frac{3x}{1-2x^2})+\pi ,\frac{\sqrt{2}}{2}\le x\le1 qui est continue sur[0,1] et dont une primitive sur[0,1] est:
G(x)=\{{xarctg(\frac{3x}{1-2x^2})-\frac{1}{2}ln(x^2+1)-\frac{1}{4}ln(4x^2+1) , 0\le x\le\frac{\sqrt{2}}{2}\\xarctg(\frac{3x}{1-2x^2})-\frac{1}{2}ln(x^2+1)-\frac{1}{4}ln(4x^2+1)+\pi x ,\frac{\sqrt{2}}{2}\le x\le1 et on peut maintenant écrire que:
\int_{0}^{1}g(x)dx=G(1)-G(0)=\pi-arctg(3)-\frac{1}{2}ln(2)-\frac{1}{4}ln(5) et voilà il ne reste plus qu'à remarquer que:
\int_{0}^{1}g(x)dx=\int_{0}^{1}arctg(\frac{3x}{1-2x^2})dx+\int_{\frac{\sqrt{2}}{2}}^{1}\pi dx pour déduire finalement que:
3$\blue\int_{0}^{1}arctg(\frac{3x}{1-2x^2})dx=\pi\frac{\sqrt{2}}{2}-arctg(3)-\frac{1}{2}ln(2)-\frac{1}{4}ln(5)

Posté par jmix90 (invité)re : Primitive... 18-08-05 à 08:05

D'accord alors...

Merci !


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1675 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !