Inscription / Connexion Nouveau Sujet
primitive de fonction racine cubique
Bonjour,
Je dois trouver la primitive de la fonction : racine cubique (1+x^3) en passant par des chagements de variables.
Ex: t=1/x ; u=t^3 ; v=racine cubique (1+u)
Pouvez-vous m'éclairer pour ces changements de variables car je dois me retrouver avec des dx et dt et je ne comprends pas ?
Merci.
y a un truc qui cloche
tu veux pas plutôt intégrer racine cubique de ,
sinon je comprends pas pourquoi tu passerais à la variable t = 1/x.
Bonjour benji056
tu devrais bien relire l'énoncé du problème qui t'as été posé : Il n'est certainement pas écrit exactement de la façon dont tu le présentes sur le forum.
Est-ce bien cela qui est demandé ? Est-ce que tu as vraiment besoin de connaitre les primitives de cette fonction ? Ne peux-tu pas répondre à la question sans connaitre littéralement les primitives ?
Je te dis cela parce que les primitives de racine cubique (1+x^3) sont des fonctions faisant appel à des connaissances d'un niveau très suppérieur.
A bon entendeur salut !
Bonjour,
Voici mon énoncé, je me suis peux être mal exprimé.
On cherche `a calculer une primitive de la fonction f : x  racine cubique de (1 + x^3) à l'aide de plusieurs changements de variable.
racine cubique de (1 + x^3) à l'aide de plusieurs changements de variable.
1) Sur quel domaine peut-on chercher une primitive de f ?
2) Effectuer le changement de variable t = 1/x en justifiant sa validité.
3) Poser ensuite u = t3 en justifiant de mˆeme.
4) Puis, poser v = p3 1 + u, en justifiant.
5) a) Remarquer que v/(v^3−1) = 1/3 .(( A/v−1) + ((Bv+C)/(v2+v+1))), A, B et C ´etant des constantes à
d´eterminer.
b) On ´ecrira ensuite Bv + C = B/2 .(2v + 1) + (C − B/2 ) pour mettre (Bv+C)/(v2+v+1) sous
la forme d'une somme.
6) Int´egrer les trois termes ainsi obtenus (`a l'aide d'une table).
7) En exprimant v en fonction de x, donner une primitive de f.
Merci.
erreur
Dans l'énoncé c est u=t^3 et v=racine cubique de (1+U) pour les chagements de variables..
Merci
oui, cette notion de 3 termes ( 5° et 6° ) laisse bien penser que la structure donnée à 14:53 est bonne...

Je suis desesperé car c est une Dm que j ai à rendre pour demain et je nage..help!
t = 1/x => x = 1/t
dx = -dt/t²
(1+x^3)^(1/3) = (1+1/t^3)^(1/3) = (1+t^3)^(1/3)/t
S = S(1+t^3)^(1/3)(-dt/t^3)
pose u = t^3 => du = 3t²dt = 3(u^2/3)dt => dt = du/(3u^2/3)
S = S -(1+u)^(1/3)/u (dt) = S -(1+u)^(1/3)/u (du/3u^(2/3)) = (-1/3)S (1+u)^(1/3)/(u^(5/3) . du
A vérifier, suis pas sûr

Merci beaucoup ! Je m'y replonge dedans...

Aïe, aïe, aïe, j'aurais mieux fait de me taire.
Je ne croyais pas que l'on puisse obtenir cela sans être obligé de passer par l'intermédiaire d'une fonction spéciale.
La méthode est sophistiquée en tout cas. Je tire mon chapeau à celui qui aurait trouvé tout seul, sans connaitre les changements de variables à faire !
Bonjour,
Je suis bloqué dans mon exo et je souhaiterais que quelqu'un aide.
Voilà ce que j'ai fait :
Je dois trouver la primitive de racine cubique (1+x^3).
J'ai effectué le premier changement de variable avec t=1/x :
x=1/t donc dx=-dt/t^2
en remplaçant : racine cubique ((1+(1/t^3)) . -dt/t^2
Ensuite le deuxieme changement de variable et u=t^3 :
t=racine cubique de u donc du=3t^2.dt dt=du/(3t^2)
en rmplaçant : - racine cubique ((1+u)/u) . du/(3u^2)
Après il y a un troisième changement de varible avec v=racine cubique (1+u) :
1+u=v^3 et u=v^3-1 du=1/3 . dv/(1+u)^(2/3)
en remplacçant : - v/racine cubique (v^3-1) . dv / 9 (1+U)^(2/3) . 1/(v^3-1)^2
question : comment puis je transformer (1+u)^(2/3) ??
je sais que (1+u)^1/3 = racine cubique de 1+u
HELP !
merci
*** message déplacé ***
Bonsoir 
Continue dans le topic initial, je te rappelle que le multipost n'est pas toléré.
*** message déplacé ***
Bonjour,
Je suis bloqué dans mon exo et je souhaiterais que quelqu'un aide.
Voilà ce que j'ai fait :
Je dois trouver la primitive de racine cubique (1+x^3).
J'ai effectué le premier changement de variable avec t=1/x :
x=1/t donc dx=-dt/t^2
en remplaçant : racine cubique ((1+(1/t^3)) . -dt/t^2
Ensuite le deuxieme changement de variable et u=t^3 :
t=racine cubique de u donc du=3t^2.dt dt=du/(3t^2)
en rmplaçant : - racine cubique ((1+u)/u) . du/(3u^2)
Après il y a un troisième changement de varible avec v=racine cubique (1+u) :
1+u=v^3 et u=v^3-1 du=1/3 . dv/(1+u)^(2/3)
en remplacçant : - v/racine cubique (v^3-1) . dv / 9 (1+U)^(2/3) . 1/(v^3-1)^2
question : comment puis je transformer (1+u)^(2/3) ??
je sais que (1+u)^1/3 = racine cubique de 1+u
HELP !
merci

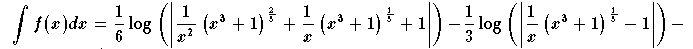
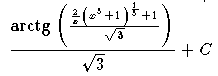


 analyse en Bts
analyse en Bts