Inscription / Connexion Nouveau Sujet
Primitive de ln(ln x)
Bonjour,
Tout est dans le titre 
Je cherche la primitive de ln(ln x).
J'ai essayé pas mal de méthode (IPP, changement de variable...) mais je bloque...
Merci 
salut,
on ne peut pas exprimer les primitives avec des fonctions usuelles.
Maple dit : ln(ln(x))*x+Ei(1,-ln(x)) (Ei : intégrale exponentielle)
C'est un exercice pour un devoir... pourquoi ?
J'ai aussi une autre intégrale, peut être plus simple : t^2 * Arctan(t)^2
par parties... tu primitives t² et tu dérives arctan(t²)... tu récupères une fraction rationnelle à intégrer... virtuellement terminé !
MM
Elle est continue sur ]1,+oo[ donc elle y admet une infinité de primitives ... mais qu'on ne sait pas exprimer avec les fonctions usuelles.
Si ça se trouve l'exo ne demande pas un calcul explicite .. 
L'enoncé est : Calculer les primitives suivantes : ln(ln(x)) 
Apparemment, il faut trouver un truc :
comme en pièce jointe...
J'ai fais une première IPP et j'ai trouvé :
A = x*ln(ln x) -  (1/ln t) dt
(1/ln t) dt
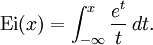


 analyse en post-bac
analyse en post-bac