Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Licence Maths 1e ann AnalyseTopics traitant de analyse [tout]Lister tous les topics de mathématiques
Niveau Licence Maths 1e ann
Primitives
Posté par ausensio45
Bonjour,
J'aimerais déterminer une primitive de à l'aide d'un changement de variable.
Merci d'avance
Bonjour,
pas vraiment, t2 ne réalise pas un difféomorphisme avec ]-1,+
[. Le mieux c'est de prendre u = e^x et de refaire un changement de variable après.
.Sans changement de variable ni calcul d'intégrale
Citation :
![\dfrac{1}{\sqrt{e^x-1}} = 2\dfrac{1}{e^x} \times \left[\dfrac{1}{2\sqrt{e^x-1}} \times e^x\right]](https://latex.ilemaths.net/ile_TEX.cgi?\dfrac{1}{\sqrt{e^x-1}} = 2\dfrac{1}{e^x} \times \left[\dfrac{1}{2\sqrt{e^x-1}} \times e^x\right])
La partie entre crochets est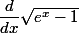
et le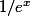 
correspond à )
.
La formule de dérivation d'une composée de fonctions nous dit donc qu'une primitive de la fonction que tu demandes est donnée par = 2\arctan(\sqrt{e^x-1}))
.
La partie entre crochets est
La formule de dérivation d'une composée de fonctions nous dit donc qu'une primitive de la fonction que tu demandes est donnée par
Calcul en utilisant ce résultat.
Citation :
Sa forme suggère de poser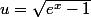
, ce qui est parfaitement inversible sur ![]0,\infty[](https://latex.ilemaths.net/ile_TEX.cgi?]0,\infty[)
, qui est le domaine de définition de la fonction à intégrer, très régulier, et strictement croissant.
Ca correspond à)
, et )
. À une constante près,
 = \int_0^u \dfrac{1}{\sqrt{e^x-1}}\text{d}x = \int_{0}^{\sqrt{e^u-1}} 2\text{d}(\arctan u) = 2\arctan(\sqrt{e^u-1}) )
Sa forme suggère de poser
Ca correspond à
Annuler
connectez vous
analyse en post-bac