commence par regarder le cas où u : [a , b]   est continue et f  : [a , b]   vérifie f(a) 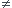u(a) et f(x) = u(x) pour x dans ]a , b] .

Bonjour coa347.
Pour des fonctions continues par morceaux, il faut renoncer à obtenir une formule du genre F' = f. C'est mort sur les discontinuités de f.
Donc, au mieux, on a des primitives par morceaux au sens classique.
Si le livre parle de "en général", c'est pour signifier qu'au sens classique, c'est mort, mais qu'il existe d'autres type de "primitives"; (à mon avis ça ne doit pas être à ton programme.)

Hello!

Si tu prends f(x) = 2xsin(1/x) - cos(1/x), alors f n'est pas continue mais admet comme primitive F(x) = x²sin(1/x) (avec F(0) = 0)

Merci pour vos réponses.

@lionel52 J'ai bien pensé à cette fonction, mais f n'est pas continue par morceaux car elle n'admet pas de limite ni à gauche ni à droite en 0.

@etniopal De ce que je comprends, si f admettait une primitive sur [a,b], elle serait égale (à une constante près) à celle de u (puisqu'elle ne diffère que d'un point isolé), et ceci est impossible car leurs dérivées seraient distinctes en a.

@jsvdb Donc f peut admettre des primitives mais pas au sens donné plus haut F'=f. Dans ce cas-là, c'est impossible. Oui elle admet des primitives sur les intervalles où elle est continue, mais pas sur l'intervalle où elle est continue par morceaux.

Je trouve tout ça assez compliqué. Le problème c'est qu'il existe des fonctions dérivables de dérivée non continue comme la sempiternelle f(x)=x^2*sin(1/x). A ce propos, existe-t-il d'autres exemples de fonctions dérivables de dérivée non continue ?

Tout à fait, il est dommage de ne pas pouvoir "primitiver" la fonction d'Heaviside juste pour un soucis en 0.
Le principe repose sur le fait que si une fonction est dérivable au sens classique, alors sa dérivée est continue presque partout au sens de Lebesgue.
C'est un problème assez ardu.
Mais sinon, tu peux retenir déjà ceci :  pas continue au sens classique = pas de primitive sur l'ensemble de définition.
Pour voir, par exemple, le soucis avec la fonction 2xsin(1/x) - cos(1/x), c'est que tu ne peux pas définir f en 0 de sorte que F'(0) = f(0)

Mais la fonction 2x*sin(1/x)-cos(1/x) nulle en 0 n'est pas continue en 0, mais elle admet pourtant une primitive sur R : x^2*sin(1/x) ?

Tout le problème est là : si toutes les fonctions dérivables sur un intervalle étaient continues sur cet intervalle, on pourrait dire qu'une fonction admet une primitive ssi elle est continue. Mais il y a des fonctions non continues (pas les continues par morceaux) qui admettent des primitives.

Effectivement, je me suis emmêlé les pinceaux !

Cette fonction F(x) = x² sin(1/x) pour x 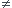0, et F(0) = 0 fait bien partie de celles que j'ai décrites comme ayant une dérivée presque partout continue.
On a bien F'(x) = 2x*sin(1/x)-cos(1/x) pour x 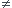0 (indiscutable), et on pose F'(0) = 0 pour que F soit une primitive de F'.

Là où j'ai confondu, c'est avec le fait que F(x), x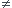0 ne s'écrit pas comme l'intégrale de 0 à x de F'.

Alors qu'à contrario, la fonction x |x| peut s'écrire comme l'intégrale de sa "pseudo-dérivée" : la fonction signe de x. (nulle en 0 par exemple)

Tout ceci ne contredit en rien le premier théorème de l'analyse qui dit que toute fonction continue f sur un domaine [a,b] admet des primitives qui sont données par :

telles que

Après, si f n'est plus continue, c'est du cas par cas :

- f admet des primitives, mais qui ne s'écrivent pas sous forme intégrale.
- f admet des primitives qui s'écrivent sous forme intégrale, mais alors f n'est plus la dérivée de F

Bonsoir !
J'ai lu çà

luzak, la notion dont tu parles est un cas particulier de celle de fonctions absolument continues.

On dit qu'une fonction est absolument continue si, pour tout réel , il existe un tel que, pour toute suite de sous-intervalles de I d'intérieurs disjoints :



On a alors que les proposition suivantes sont équivalentes :

1- F est absolument continue sur [a, b]
2- Il existe une fonction f intégrable sur [a, b] (au sens de Lebesgue) telle que pour tout

Ou bien encore :
1- F est absolument continue sur [a, b] équivaut à
2- i)   F est continue ;
      ii)  F est à variation bornée (donc dérivable presque partout) ;
      iii) L'image par F de tout ensemble de mesure nulle (pour la mesure de Lebesgue) est de mesure nulle.

On peut donc voir F comme une "primitive en un sens très large" de f :
c'est que j'ai appelé dans mon post de 10:11 " d'autres type de "primitives" "
( @coa347 : il y en a encore d'autres, mais on sort un peu du contexte des intégrales )

D'après le second théorème fondamental de l'analyse, si (sur [a, b]) F est dérivable partout et de dérivée intégrable, alors F est absolument continue.

Exemple : Toute fonction lipschitzienne sur [a, b] est absolument continue.

Contre-exemple : La fonction continue qui a pour graphe l'escalier du diable n'est pas absolument continue : l'image de l'ensemble de Cantor, qui est de mesure nulle, est [0,1] tout entier.

Bonsoir,

@jsvdb Je ne comprends pas pourquoi la fonction x^2*sin(1/x) ne peut pas s'écrire sous forme d'intégrale de sa fonction dérivée 2x*sin(1/x)-cos(1/x) nulle en 0 continue sur R ?

La notion de fonction absolument continue (et de mesure de Lebesgue) m'est inconnue.

@luzak Merci pour ta réponse. Oui j'ai fourché, je voulais dire, mais tu l'auras compris certainement, "si toutes les fonctions dérivables étaient de dérivée continue".

Je crois bien comprendre l'intérêt de "primitive au sens large". On veut donner par exemple aux fonctions continues par morceaux, des primitives dérivables presque partout (sauf en un nombre fini de points) parce qu'on peut exprimer leur aire sous la courbe à l'aide d'une intégrale.

Maintenant je me pose une question toute bête : est-ce que le problème des fonctions dérivables à dérivée non continue est le même que celui des fonctions non continues auxquelles on veut donner des primitives, ou cela n'a rien à voir ?

Bonjour,

En définitive, ce que je comprends c'est que les fonctions réelles continues par morceaux sur un intervalle I, mais non continues sur I :
  - admettent des primitives sur les intervalles où elles sont continues (enfin leur restriction ...)
- n'admettent pas de primitives au sens usuel sur l'intervalle tout entier I (à cause  des points de discontinuité où leurs primitives ont des dérivées à gauche et  droites distinctes)
- admettent des primitives au sens général sur I, car la fonction intégrale (aire sous la courbe) est continue, non dérivable partout ; si on ne s'intéresse qu'à l'aire, ceci n'a pas d'importance.

primitive "au sens général", je voulais dire "au sens large".

Pour ta question sur l'égalité lorsque le tout est de savoir comment tu définis l'intégrale d'une fonction discontinue en un point.

Si tu connais l'intégrale de Riemann : une fonction bornée et continue sauf sur un ensemble fini (j'abrège : ensemble négligeable marche aussi) est intégrable et, si on connait une primitive au sens large, il y a égalité entre l'intégrale et la différence des valeurs de la primitive.

Si tu ne veux manipuler QUE les intégrales des classe prépas, ça marche aussi car la fonction bien que non continue par morceaux est intégrable (définition prépas : continue par morceaux sur les segments de et  ensemble majoré des intégrales sur les segments de la valeur absolue).

Si tu as une autre définition de "intégrale" il faut voir !

Ah oui, merci luzak, je me suis encore emmêlée. Je comprends pour la fonction x^2*sin(1/x), sa dérivée n'est pas continue en 0, ni même continue par morceaux, donc au sens prépa (de ce que j'en connais), on ne sait pas définir l'intégrale de la fonction avec l'intégrale de Riemann.

En effet, en prépa, l'intégrale de Riemann n'est définie que pour les fonctions continues par morceaux.

Du coup ça commence à s'éclairer : le problème de cette fonction dérivable de dérivée non continue ni même continue par morceaux non intégrable au sens de Riemmann n'a rien à voir avec le problème des fonctions continues par morceaux qui sont intégrables mais qui n'admettent pas de primitive sur tout l'intervalle.

Mais si j'ai bien compris, ton propos est de dire que même cette fonction est intégrable (à un sens que j'ignore).

Evidemment dans mon post précédent, quand je parle de l'intégrale de la fonction x^2*sin(1/x), je parle de l'intégrale de sa dérivée.

Il me manque des exemples de fonctions dérivables de dérivée non continue. En avez-vous d'autres ? Merci d'avance.

Je cherche vainement un exemple de fonction dérivable à dérivée non continue mais continue par morceaux. Mais peut-être est-ce impossible ?

Je reviens sur la fonction (je ne reprécise plus ).
Cette fonction est dérivable partout et de dérivée Lebesgue-intégrable sur [-1;1]
En effet, la dérivée est continue sur donc elle est mesurable sur donc sur [-1;1]
Elle est de plus bornée sur [-1;1] donc intégrable donc sur [-1;1]

Par conséquent, l'expression a un sens pour

D'après le second théorème fondamental de l'analyse, si (sur [-1, 1]) F est dérivable partout et de dérivée intégrable, alors F est absolument continue.

Il s'ensuit de la caractérisation des fonctions absolument continues qu'il existe une fonction Lebesgue intégrable sur [-1;1], telle que pour tout ,

Or, si pour tout , et toute fonction intégrables Lebesgue on a alors p.p.

Conclusion -presque partout et donc, au sens de l'intégrale de Lebesgue, on a :

.

Par extension, cette formule sera valable pour tout .

Mais je pense que ce raisonnement doit largement dépasser le programme de prépa car je ne suis pas sûr que soit Riemann-intégrable.

Mais si voyons : il y a une seule discontinuité et la fonction est bornée.
Elle est non seulement Riemann-intégrable mais aussi "prépa"-intégrable (continuité sur l'intervalle ouvert, et l'ensemble des admet une borne supérieure).

En fait, F', bien que non réglée sur [-1;1] est bien intégrable Riemann... ok

Ok, luzak, vu  ... (on s'est télescopé)

Du coup, on doit pouvoir écrire  .

En revanche, ce ne sera pas le cas avec la fonction qui, elle, ne s'écrira pas comme l'intégrale de sa dérivée (ça j'en suis sûr... que ce soit Lebesgue ou Riemann) !

On peut quand même écrire pour .

Ce sont les intervalles admettant 0 à l'intérieur qui posent problème.

Bonjour luzak,

Dans mon cours de prépa, pour la définition de l'intégrale de Riemann, je ne connais pour l'instant que celle des fonctions bornées et continues sauf sur un ensemble fini de points. Du coup, je ne peux pas comprendre la généralisation de "intégrale au sens de Riemann", terme que j'ai employé un peu abusivement.

Sinon, je m'étais entre-temps démontré qu'il était impossible qu'une fonction continue, dérivable, soit de dérivée continue par morceaux.

Par exemple (généralisable), la fonction continue et dérivable dont la dérivée qui prend la valeur 1 sur R+ et la valeur -1 sur R-*. Sa primitive (continue) est égale à x+b sur R+ et -x+b sur R-*. Donc sa dérivée à droite en 0 est 1, et à gauche en 0 (d'après le théorème de la limite de la dérivée appliqué à R-, ou bien démontré directement) est -1. Elle n'est donc pas dérivable en 0.


Du coup, je comprends beaucoup mieux ce que je ne comprenais pas au début. A savoir pourquoi certaines fonctions continues et dérivables pouvaient ne pas être de dérivée continue (je croyais que c'était parce que leur dérivée était seulement continue par morceaux. Et en fait pas du tout, c'est parce que leur dérivée n'a aucune limite en un point). Merci !

Un bémol concernant

Oui, il était sous-entendu que la fonction était à valeurs réelles (je l'avais dit tout en haut), et effectivement je voulais dire "dont la dérivée soit seulement continue par morceaux (et pas continue)", car le "seulement" me paraissait évident.

Ceci dit pour trouver une autre fonction de ce genre-là, cela ne doit courir les rues.

1. Je n'ai pas vu de "seulement" dans la phrase que je conteste (je veux bien changer de lunettes mais de toute façon ce ne serait pas une rédaction correcte, sauf à ajouter "non continue", comme tu le fais).
2. Sois précis(e) : que veut dire "une autre fonction de ce genre-là" ? Et pourquoi en faut-il "une autre" ? Quand on a un contre-exemple, en avoir une multitude ne sert à rien !

Les choses seraient plus simples si on pouvait dire que toutes les fonctions dérivées sont continues. Je trouve cela dommage de se restreindre pour une seule fonction (un seul type de fonction, j'imagine que la fonction x^2*cos(1/x) et d'autres du même style, est dans le même cas). Il faut que le taux d'accroissement de la fonction en un point ait une limite finie mais que les accroissements tout autour ne tendent pas vers cette limite, et tout ceci bien que la fonction soit continue. Je ne vois pas d'autres fonctions que les fonctions trigonométriques qui peuvent se comporter comme ça. Mais en effet pourquoi pas ?

Je crois que les mathématiciens du 18ème siècle ont mis du temps à admettre ce genre d'"anomalies".

Mais il y a plein de fonctions dérivées qui ne sont pas continues, la dérivée de en est une.
Bien entendu elles ne courent pas les rues mais les exemples bâtis avec les fonctions trigonométriques n'en ont pas l'exclusivité.

Ce ne sont pas des fonctions dérivées non continues qui ont chagriné certains mathématiciens au départ, mais plutôt l'existence de fonctions continues non dérivables (il leur était difficile d'imaginer de pouvoir tracer une courbe "continue" sans mettre de tangentes).
Poincaré disait : "je me détourne avec horreur de la plaie des fonctions continues non dérivables". Il savait bien reconnaître qu'elles existaient mais leur existence le choquait.

Et Visiblement dans l'éducation nationale on a l'air d'avoir la même difficulté d'imagination ( ce qui n'est pas fait pour me surprendre ).  Une fonction continue est une fonction qu'on ne peut pas définir autrement que par un «  tracé sans lever le crayon ».  Un peu léger à mon goût .  Ça vous plante des images d'Épinal dans le crâne de pas mal de lycéens et c'est assez coton à supprimer.

Pour pimenter un peu le tout, sache qu'il existe des fonctions dérivables,  de dérivée bornée, et dont ladite dérivée n'est pas intégrable. Ça tient de la sorcellerie.
Donc tout ceux qui me disent que dériver et intégrer sont deux opérations inverses l'une de l'autre... Je réponds : FAUX.

Bonjour,

Voici le lien que je cherchais (exemples de dérivées non continues) :http://forum.prepas.org/viewtopic.php?f=3&t=48252

Cela renvoie sur un autre lien. Ces fonctions sont des fonctions de Darboux, qui vérifient le TVI sans être continues.

Poincaré était choqué par les fonctions continues nulle part dérivables (@luzak je te renvoie la balle, à ta formulation, j'ai pensé d'abord "non dérivables en un point" ). Mais ceci me choque bcp moins que les dérivées non continues.

Les exemples de ton lien utilisent encore des fonctions trigonométriques. Je croyais que tu voulais t'en affranchir ?

Bonjour,

@jsvdb Oui c'est vrai. Plus précisément c'est le "tiré par les cheveux" qui l'est plus ou moins.

En fait, cette fonction x^2*sin(1/x), on serait incapable de la tracer autour de 0. Elle est continue en 0 selon la définition mathématique, mais pas au sens où on le perçoit habituellement "sans lever le crayon".

Une fonction dessinée "sans lever le crayon", si elle était dérivable, serait évidemment de dérivée continue.

Tout cela pour dire que cette bizarrerie de dérivée non continue provient donc de la définition de la continuité (on se rapproche aussi près que l'on veut de l'image) qui ne coïncide pas avec l'idée que l'on s'en fait.