Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Maths sup ProbabilitésTopics traitant de probabilités [tout]Lister tous les topics de mathématiques
Niveau Maths sup
Partager :

Proba

Posté par elaure (invité) 02-11-05 à 12:02

Bonjour, j'ai un énorme exo de proba à faire et je bloque sur certaine questions qui sont assez compliqué je trouve, je vous indique au cours de l'exercice où je suis bloquée.

Jet simultané de deux dés non pipés
on lance simultanément deux dés non pipés et on note S la varaible égale à la somme des deus dés, donner la loi de S, calculer son espéance et sa variance.
Ok pour cette question

Le jeu du craps est une succession de jets simultanés de deux dés discernables par exemple de couleurs différentes et non pipés. Au jet n, on associe la variable aléatoire Sn égale à la somme des deux dés, les variables aléatoires Sn suivent la loi de S variable définie plus haut.
Le premier jet est particulier
si S1=7 ou 11 le joueur  gagne et le jeu s'arrete
si S1=2,3 ou12 le joueur perd et le jeu s'arrete
si S1= 4,5,6,8,9,ou10 le joueur reprend les dés et effectue le second jet.
A partir de la , le joueur ralance les dés et pour tout ebtier n>=2:
si le nième lancer a lieu , on note Sn la variable aléatoire égale à la somme des deux dés et
si Sn=S1 le joueur gagne et le jeu s'arrete
Si Sn=7 le joueur perd et le jeu s'arrete
sinon il reprend les dés et effectue le jet suivant
L'objectif du joueur est ainsi de reproduire le valeur obtenur au permier lancer avant de réaliser 7.
a) Soit k appa {4,5,6} montrer que P[S2=k]sachan[S1=k]=(k-1)/36
ok pour cette question
b) Soit k app {4,5,6} montrer que pour n>=2 : P[Sn=k]sachan[S1=k]=(k-1)/36 *((31-k)/36))^(n-2), la j'ai un problème j'arrive pas à trouver le 31 je ne trouve pas mon erreur ...
c) On note G le joueur gagne
montrer que pour k app {4,5,6} P(G)sachant[S1=k]=(k-1)/(k+5) ok
d) calculer de meme P(G)sachant[S1=k] pour k app{8,9,10} la je bloque
e) Soit G' le joueur gagne au premier jet. Déterminer la probabilité de G'. je pense que c'est l'addition de la réponse c et d?
f) Soit G'' le joueur gagne après le premier jet. Montrer que P[G'']=2sum(k-1)/(k+5)*((k-1)/36) de k=4à6 la je suis bloqué
g) Détermiber enfin p(G) et vérifier que le craps n'ets pas un jeu trop voleur c'est à dire que la probabilité pour le joueur de gagner est très peu inférieure à 0.5 ok

Jeu en famille finie
sur cette partie je bloque vraiment
Plusieurs joueurs nommés J1...Jn jouent l'un après l'autre dans l'ordre des indices.
A chaque joueur J1...Jn est imparti un evt A1..An
Le jeu se terminer quand l'un des joueurs réalise l'evt aléatoire qui lui est imparti: auquel cas il gagne.
Quand aucun des joueurs n'a gagné, on recommence un tour et on continue ainsi jusqu'à ce que l'un des joueurs gagne. Ainsi un joueur qui n'a pas gagnée à sont tour peut avoir à nouveau la main et n'est pas éliminé (immédiatement)/
on désignera par pk la probabilité non nulle pour le joueur Jk de réaliser l'evt Ak quand il a la main. On posera qk=1-pk et q0=1. levt Jk gagne sera noté Gk et on supposera l'indépendance, mutuelle à priori, de toutes les suites de résultats des coups joués par les concurrents jusqu'à la fin de la partie si tant est qu'elle se termine.
Entre deux joueurs J1 et J2
a)Remarquer que J1 ne peut jouer qu'aux rangs impairs et J2 au rangs pairs.(dois je répondre à cette remarque) En déduire que P(G1)=sum(q1q2)^n*p1 pour n=0à+inf=p1/(1-q1q2) je trouve la deuxième égalité mais pas la première.pareil pour G2: P(G2)=sum(q1q2)^n*q1p2 pour n=0à+inf=q1p2/(1-q1q2)
Calculer P(G1)+P(G2) ok et en déduire que le jeu se termine de facon certaine au bout d'un nombre fini de coups. la je sais pas comment faire
b) On désigne par T la variable aléatoire égale au nombre de coups joués jusqu'à la fin du jeu; montrer que l'espérance E(t)=(2-p1)/(1-q1q2)  j'y arrive pas
c) on dit que le jeu est équitable si P(G1)=P(G2) Montrer que le jeu est équitable si et slt si p2=p1/(1-q1q2) je n'arrive pas à trouver ca
d) Exprimer E(T) dans le cas où le jeu est équitable. la aussi je suis bloqué

Entre c joueurs ( pour cette partie je n'ai trouvé aucune question c'est la cata)
a)Expliquer pourquoi pout tout k appa {1,2,...c} le joueur Jk ne peut éventuellemnt jouer (et gagner) qu'aux rangs (cn+k) où n est un entier naturel et que P(Gk)=q0q1...qk-1qk*sum(q0q1..qc)^n pour n=0 à +inf
b) démontrer que sum q0q1...qk-1qk+q0q1...qc(de k=1 à c)=1 et en déduire que le jeu se termine de facon certaine au bout d'un nombre fini de coups.
c) On dit que le jeu est équitable si pour tout k app {1...C} P(Gk)=1/c
montrer que le jeu est équitable si et slt si pour tout k appa {1...c-1} p(k+1)=pk/(1-pk)
On pose Rk=1/pk et on suppose le jeu équitable, déterminer rk, puis pk en fonction de k et de p1. En déduire que si le jeu est équitable alors p1<=1/c Déterminer pc quand le jeu est équitable et que p1=1/c
d) La varaible T étant définie comme dans la compétition entre deux joueurs montrer que dans le cas d'équiprobabilité on a E(T)=sum iP(T=i)de i=1 àinf=1/p1-(c-1)/2 (on pourra remarquer que q0q1...qc=1-cp1)
j'ai encore une troisième partie, qui me semble necore plus complqié mais pour auj je pense que y en a assez!
Merci d'avance.

Posté par elaure (invité)re : Proba 02-11-05 à 18:39

y a t'il quelqu'un qui puisse me consacrer un peu de temps?

Posté par
franzre : Proba 02-11-05 à 21:51

Exo I b)

L'événement [Sn=k]sachant[S1=k] revient à dire que les lancers 2,3,...,n-1 ont donné des résultats S_i différents de 7 et de k.
Sur les 36 lancers possibles, il existe 6 lancers qui conduisent à un total de 7 et k-1 qui conduisent à un total de k donc
\Large p_{(S_{i-1}\notin \{k,7\})}(S_i\notin \{k,7\})=1-\(\frac {6}{36}+\frac {k-1}{36}\)=\frac {31}{36}
et par la suite
\Large p_{(S_1=k)}(S_n=k)=\left(\frac {31}{36}\right)^{n-2}\,\left(\frac {k-1}{36}\right)

Posté par
franzre : Proba 02-11-05 à 21:57

Désolé, j'ai fait des copier-coller malencontreux. Il faut bien sûr lire

\Large p_{(S_{i-1}\notin \{k,7\})}(S_i\notin \{k,7\})=1-\(\frac {6}{36}+\frac {k-1}{36}\)=\frac {31-k}{36}

et

\Large p_{(S_1=k)}(S_n=k)=\left(\frac {31-k}{36}\right)^{n-2}\,\left(\frac {k-1}{36}\right)

Posté par
franzre : Proba 02-11-05 à 22:02

Exo I d)

En constatant que \Large \forall k\in\{2,...,12\}\;,\;p(S_i=k)=p(S_i=14-k)
Les résultats de 8,9,10 sont identiques à ceux de 4,5,6 respectivement.

Posté par
franzre : Proba 02-11-05 à 22:21

Exo I e)

\Large p(G^')=p(S_1\in\{7,11\})=\frac {6}{36}+\frac {2}{36}=\frac {2}{9}

Exo I f)

\large \array{ccl$ p(G^{''}) & = & p(G\cap \[S_1\in\{4,5,6,8,9,10\}\]) \\ & = & \Bigsum_{k\in\{4,5,6,8,9,10\}}p_{(S_1=k)}(G).p(S_1=k)\\ & = & 2\,\Bigsum_{k=4}^6 p_{(S_1=k)}(G).p(S_1=k)\hspace{25}{\rm de par la symetrie du Ie)}\\ & = & 2\,\Bigsum_{k=4}^6 \frac {k-1}{k+5}\frac {k-1}{36}\\ &=& \LARGE \frac {134}{495} }


Exo I g)
\Large p(G)=p(G^')+p(G^{''})=\frac {244}{495}\approx 0,493

Posté par
franzre : Proba 02-11-05 à 22:37

Exo II a)

\large p(G_1)=p\(\Bigcup_{k=0}^{\infty}A_{2k+1}\)=\Bigsum_{k=0}^{\infty}p\(A_{2k+1}\)

Or
\large \array{ccl$p\(A_{2k+1}\) & = & p\(\bar{A_{1}} \cap \bar{A_{2}} \cap \bar{A_{3}}\cap...\cap\bar{A_{2k}}\cap A_{2k+1}\)\\ & = & q_1\,q_2\,q_1\,...q_2\,p1 \\ & = & (q_1q_2)^kp_1

Donc
\large p(G_1)=\Bigsum_{k=0}^{\infty}(q_1q_2)^kp_1=\Large \frac {p_1} {1-q_1q_2}


Même chose pour J_2 (mais attention aux indices)

\large p(G_2)= \Bigsum_{k=1}^{\infty}p\(A_{2k}\) = \Bigsum_{k=1}^{\infty}q_1(q_2q_1)^{k-1}p_2 = \Large \frac {q_1p_2} {1-q_1q_2}

Posté par
syrahGéométrie 02-11-05 à 22:49

Bonsoir,
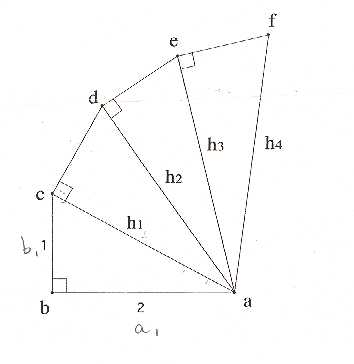
En étudiant les triangles ci-dessous, on doit trouver la dimension de la 103e hypothénuse:

J'ai trouvé que, par les triangles semblables, H1/a1 = H2/H1 =H3/H2=...= de/cd=cd/bc. J'ai intuitivement trouvé que bn= (H1/A1)n-1 où n est le nombre de triangles,
et que hn= 2 (H1/A1)n.
J'ai donc trouvé la 1a méthode pour calculer la nième hypothénuse.Mais la formulation me semble un peu difficile.
Mais je dois encore trouver la relation entre les polygones:
bac, badc, baedc, bafedc,........
Quelqu'un peut m'aider?

Géométrie

Posté par
franzre : Proba 02-11-05 à 23:19

Exo 2b)

p(T=k)=p(A_k)

Il faut distinguer les cas pair et impairs comme au a).
\large \array{ccl$ E(T) & = & \Bigsum_{k=1}^\infty k p(T=k) \\ & = & \Bigsum_{k=0}^\infty (2k+1) p(T=2k+1)\,+\,\Bigsum_{k=1}^\infty 2k\, p(T=2k) }

\large \array{ccl$ \Bigsum_{k=0}^\infty (2k+1) p(T=2k+1) & =& \Bigsum_{k=0}^\infty (2k+1)(q_1q_2)^k p_1 \\ & = & 2p_1\, \Bigsum_{k=0}^\infty k(q_1q_2)^k \;+\; p_1\, \Bigsum_{k=0}^\infty (q_1q_2)^k \\ & = & 2p_1\,\frac{q_1q_2}{(1-q_1q_2)^2} \;+\; p_1\,\frac 1 {1-q_1q_2} \vspace{55}\\ & = &\Large p_1\,\frac {1+q_1q_2}{(1-q_1q_2)^2} }

\large \array{ccl$ \Bigsum_{k=1}^\infty (2k) p(T=2k) & =& \Bigsum_{k=1}^\infty (2k)(q_1q_2)^{k-1} q_1p_2 \vspace{55}\\ & = &\Large\frac {2q_1p_2}{(1-q_1q_2)^2} }

\large \array{ccl$ E(T)& = & p_1\,\frac {1+q_1q_2}{(1-q_1q_2)^2}+\frac {2q_1p_2}{(1-q_1q_2)^2} \vspace{45} \\ & = & \frac{(1-q_1)(1+q_1q_2)+2q_1(1-q_2)}{(1-q_1q_2)^2} \vspace{45} \\ & = &\frac{1+q_1-q_1q_2-q_1^2q_2}{(1-q_1q_2)^2} \vspace{45} \\ & = & \frac{(1+q_1)(1-q_1q_2)}{(1-q_1q_2)^2} \vspace{45} \\ & = & \frac{1+q_1}{1-q_1q_2}\vspace{55} \\ & = & \Large\frac{2-p_1}{1-q_1q_2} }

Posté par
franzre : Proba 02-11-05 à 23:28

Exo II a) et c)

Un petit oubli
\Large p(G_1)+p(G_2)=\frac{p_1}{1-q_1q_2}+\frac{q_1p_2}{1-q_1q_2}=\frac{1-q_1}{1-q_1q_2}+\frac{q_1(1-q__2)}{1-q_1q_2}=1

Le jeu a forcément un gagnant, l'événement \bar{G_1\cup G_2} étant impossible.

Si le jeu est équitable, \Large p(G_1)=p(G_2) donc \Large \frac{p_1}{1-q_1q_2}=\frac{q_1p_2}{1-q_1q_2}\;\Longrightarrow \; p_2=\frac{p_1}{q_1}

Posté par
franzre : Proba 02-11-05 à 23:36

Exo II e)

Dans le cas équitable, q_2=1-\frac {p_1}{q_1}=\frac {1-2p_1}{q_1}\Longrightarrow q_1q_2=1-2p_1\Longrightarrow 1-q_1q_2=2p_1

\Large E(T)=\frac{2-p_1}{2p_1}=\frac{1}{p_1}-\frac 1 2

Posté par elaure (invité)re : Proba 03-11-05 à 19:48

merci beaucoup de m'avoir autant aidé, je vais regardé si je comprends tout ça, il reste donc la dernière partie que j'ai mise "entre c joueurs" où je suis encore bloquée et une autre petite partie que je mettrais éventuellement plus tard si je bloque. (j'y ai pas encore réfléchi).
Par contre entre c joueurs, j'ai pas avancé je suis bloqué j'arrive pas à avancer, pouvez vous me donner un petit coup de pouce.
Encore merci

Posté par
franzre : Proba 03-11-05 à 22:01

Exo III a)

Ce n'est pas bien difficile, les joueurs jouant dans un ordre bien déterminé.
Le 1° joueur joue au 1° , n+1° , 2n+1°..., c n +1° coup
Le 2° joueur joue au 2° , n+2° , 2n+2°..., c n +2° coup
...
Le k° joueur joue au k° , n+k° , 2n+k°..., c n +k° coup
...
Le n° joueur joue au n° , 2n° , 3n°..., (c+1)n° coup



Pour que le k° joueur gagne au  cn+k° coupil faut que tous les coups précédents aient conduit à des échecs et que le cn+k° tour soit un succès. le nombre "c" représente le rang du tour .

la probabilité de cet événement vaut
p(A_{cn+k})=\underbrace{(q_1q_2\cdots q_n)}_{\rm 1^\circ tour}\underbrace{(q_1q_2\cdots q_n)}_{\rm 2^\circ tour}\cdots \underbrace{(q_1q_2\cdots q_{k-1}\large p_k)}_{\rm c^\circ tour}=\(q_1q_2\cdots q_n\)^{c-1}\(q_1q_2\cdots q_{k-1}p_k\)
donc
\large p(G_k)=\Bigsum_{c=1}^\infty p(A_{cn+k})=\Bigsum_{c=1}^\infty \(q_1q_2\cdots q_n\)^{c-1}\(q_1q_2\cdots q_{k-1}p_k\)=\(q_1q_2\cdots q_{k-1}p_k\)\,\frac 1 {1-q_1q_2\cdots q_n}

Posté par
franzre : Proba 03-11-05 à 22:03

Excuse moi. J'ai interverti les rôles de n et de c entre mes notations et l'énoncé
Le raisonnement reste strictement le même.

Posté par
franzre : Proba 03-11-05 à 22:34

Exo III b)

Je reviens aux notations de l'énéncé

Je pense que tu veux montrer que
\large \Bigsum_{k=1}^c p(G_k)=1 ce qui revient à prouver

\large \Bigsum_{k=1}^c \(q_1q_2\cdots q_{k-1}p_k\)=1-\(q_1q_2\cdots q_c\)
ou encore en additionnonat \(q_1q_2\cdots q_c\) aux 2 termes de l'égalité
\large \Bigsum_{k=1}^c \(q_1q_2\cdots q_{k-1}p_k\) + \(q_1q_2\cdots q_c\) =1\hspace{35}({\mathcal E})


On le montre par récurrence sur c. Le schéma est le suivant.
\large \array{cccl$\, & 1 & = & p_1+q_1 \\ \Longleftrightarrow & 1 & = & p_1+q_1\times 1 \\ \Longleftrightarrow & 1 & = & p_1+q_1\times (p_2+q_2) \\ \Longleftrightarrow & 1 & = & p_1+q_1p_2+q_1q_2 \\ \Longleftrightarrow & 1 & = & p_1+q_1p_2+q_1q_2\times (p_3+q_3) \\ \Longleftrightarrow & 1 & = & p_1+q_1p_2+q_1q_2p_3+q_1q_2q_3 \\ \vdots \\ \Longleftrightarrow & 1 & = & p_1+q_1p_2+q_1q_2p_3 + \cdots + q_1q_2...q_{k_-1}p_k+q_1q_2...q_{k_-1}q_k \\ \Longleftrightarrow & 1 & = & p_1+q_1p_2+q_1q_2p_3 + \cdots + q_1q_2...q_{k_-1}p_k+q_1q_2...q_{k_-1}q_k \times(p_{k+1}+q_{k+1}) \\\Longleftrightarrow & 1 & = & p_1+q_1p_2+q_1q_2p_3 + \cdots + q_1q_2...q_{k_-1}p_k+q_1q_2...q_{k_-1}q_k p_{k+1}+q_1q_2...q_{k_-1}q_kq_{k+1}}

Cela prouve bien l'exactitude de ({\mathcal E}) et donc le résultat.

La partie finit aubout d'un nombre fini de coups.

Posté par
franzre : Proba 03-11-05 à 22:42

Exo III c)

Si le jeu est équitable la probabilité des gains est la même pour chaque joueur.
Cela signifie
\forall k \in\{1,2,..c-1\},p(G_k)=p(G_{k+1})

\forall k \in\{1,2,..c-1\},\,\frac {q_1q_2\cdots q_{k-1}p_k} {1-q_1q_2\cdots q_c}=\frac {q_1q_2\cdots q_{k-1}q_k p_{k+1}} {1-q_1q_2\cdots q_c}

\forall k \in\{1,2,..c-1\},\,p_k=q_k p_{k+1}

\large \red \forall k \in\{1,2,..c-1\},\,p_{k+1}=\frac {q_k}{p_k}

Posté par
franzre : Proba 03-11-05 à 22:45

Euh pardon (les fautes en rouges sont encore plus visibles)

\large \red \forall k \in\{1,2,..c-1\},\,p_{k+1}=\frac {p_k}{q_k} = \frac {p_k}{1-p_k}

Posté par
franzre : Proba 03-11-05 à 22:50

Suite du III c)

\forall k \in [[1,c-1]]\;\;r_{k+1}=\frac {1-p_k}{p_k}=\frac {1}{p_k}-1=r_k-1

les termes (r_k)_{_{k\in[[1,c-1]]}} sont des termes consécutifs d'une suite arithmétique de raison (-1)

\red \forall k \in [[1,c-1]]\;\;r_{k}=r_1-(k-1)

Posté par
franzre : Proba 03-11-05 à 23:00

(Dans le post précédent, j'ai oublié le terme k=c qui est aussi compris dans la suite)


Et par la suite \forall k \in [[1,c]]\;\;\Large \red p_k=\frac 1 {\frac 1 {p_1}-k+1}

Comme tous les p_k sont compris entre 0 et 1 cela implique

\large 0\le \frac 1 {\frac 1 {p_1}-k+1}\le 1
\frac 1 {p_1}-k+1 \ge 1
\frac 1 {p_1}\ge k
\forall k \in [[1,c]] \;\; 0\le {p_1}\le \frac 1 k \;\;\Longrightarrow \;\; \LARGE p_1\le \frac 1 c

Quand p_1=\frac 1 c\;,\; p_c=\frac 1 {\frac 1 {p_1}-c+1}=1

Posté par
franzre : Proba 04-11-05 à 00:21


Je vais un peu changer les notations par rapport à celles que j'ai adoptées au III a)

n désigne le nombre de tours complets effectués et commence ainsi à 0.

l'événement A_{cn+k} correspond à n tours complets avant que le joueur k n'ait un succès et sa probabilité vaut ainsi
p(A_{cn+k})=\(q_1q_2\cdots q_c\)^{n}(q_1q_2\cdots q_{k-1}p_k)


Pour calculer l'espérance, on "range" les coups en fonction de chaque joueur comme dans le IId)

\large\array{ccl$E(T) & = & \Bigsum_{i=1}^\infty ip(A_i) \\ & = & \Bigsum_{k=1}^c \Bigsum_{n=0}^\infty (nc+k)p(A_{cn+k}) \\ & = & \Bigsum_{k=1}^c \Bigsum_{n=0}^\infty (cn+k)\(q_1q_2\cdots q_c\)^{n}(q_1q_2\cdots q_{k-1}p_k)}

Or
\large\array{ccl$\Bigsum_{n=0}^\infty (cn+k)(q_1q_2\cdots q_c\)^{n}\(q_1q_2\cdots q_{k-1}p_k) & = & (q_1q_2\cdots q_{k-1}p_k)\left[c\,\Bigsum_{n=0}^\infty n\(q_1q_2\cdots q_c\)^{n}\;+\;k\,\Bigsum_{n=0}^\infty \(q_1q_2\cdots q_c\)^{n}\right] \\ & = & (q_1q_2\cdots q_{k-1}p_k) \left[c\,\frac {q_1q_2\cdots q_c} {(1-q_1q_2\cdots q_c)^2}\;+\;k\,\frac 1 {(1-q_1q_2\cdots q_c)}\right] \hspace {45}= \hspace {45} \mathcal {(F)}_k }


Ici, un petit a parte que suugère l'énoncé:
\forall k\; q_k=1-p_k = 1-\frac 1 {\frac 1 {p_1}+1-k} = \frac {\frac 1 {p_1}-k} {\frac 1 {p_1}+1-k}

Donc q_1q_2_...q_{k-1}=\frac {\frac 1 {p_1}-1} {\frac 1 {p_1}+1-1}\times \frac {\frac 1 {p_1}-2} {\frac 1 {p_1}+1-2}\times\cdots \times \frac {\frac 1 {p_1}-(k-1)} {\frac 1 {p_1}+1-(k-1)} = \frac {\frac 1 {p_1}-1} {\frac 1 {p_1}}\times \frac {\frac 1 {p_1}-2} {\frac 1 {p_1}-1}\times\cdots \times \frac {\frac 1 {p_1}-(k-1)} {\frac 1 {p_1}-(k-2)}=\frac {\frac 1 {p_1}-(k-1)} {\frac 1 {p_1}}

ce qui conduit d'une part à
\red q_1q_2_...q_{k-1}p_k=\frac {\frac 1 {p_1}-(k-1)} {\frac 1 {p_1}}\times \frac 1 {\frac 1 {p_1}+1-k} = \frac 1 {\frac 1 {p_1}} = p_1

d'autre part à
\red q_1q_2_...q_c=\frac {\frac 1 {p_1}-c} {\frac 1 {p_1}}=1-c p_1



La somme  \mathcal {(F)}_k devient ainsi

\large \mathcal {(F)}_k = p_1 \left[c\,\frac {1-c p_1} {(1-(1-c p_1))^2} \;+\; k\,\frac 1 {1-(1-c p_1)}\right] \;=\; \frac {1-c p_1} {c p_1} \;+\;k p_1 .\frac 1 {c p_1} \;=\;\Large \(\frac{1}{c p_1}-1\)+\frac{k}{c}


Et enfin
\large\array{ccl$E(T) & = & \Bigsum_{k=1}^c \mathcal {(F)}_k \\ & = & \Bigsum_{k=1}^c \(\(\frac{1}{c p_1}-1\)+\frac{k}{c}\) \\ & = & c\(\frac{1}{c p_1}-1\) \;+\; \frac 1 c\,\frac{c(c+1)}{2} \\ & = & \frac{1}{ p_1} - c+ \frac{c+1}{2}}

                \Large \red \fbox {E(T) = \frac{1}{ p_1} - \frac{c-1}{2}}

Posté par
franzre : Proba 04-11-05 à 00:21

Ouf !!!

Posté par elaure (invité)re : Proba 04-11-05 à 20:22

merci beaucoup, je vais regarder tout ça demain après midi et si j'ai des soucis je posterai des messages sur le site.
Encore merci

Posté par margotte (invité)re : Proba 12-11-05 à 10:58

Bonjour, cet exercice m'intéresse beaucoup, du coup j'essaie de le faire mais moi je bloque dès le début comment fait on la question I a) c) et pour la d je ne comprends pas ta réponse.
Merci

Posté par margotte (invité)re : Proba 12-11-05 à 11:37

encore un petit problème, pour la question entre c joueurs b) je ne comprends pas ta réponse sachant que l'on commence à qo et pas q1 comment fait on alors?

Posté par margotte (invité)re : Proba 12-11-05 à 12:14

J'ai une suite à cet exercice que je n'arrive pas à résoudre pouvez vous m'aider?
Meme notation qu'en deuxième partie. On suppose maintenant qu'il y a une infinité de joueurs ainsi un joueur qui n'a pas gagné à son tour est définitivement éliminé et la main ne lui revient plus
on pose q0=1
a) montrer que dans ce cas le jeu ne peut être équitable et que pour tout entier on a :
P(Gn)=q0q1...qn-1pn=q0q1...qn-1-q0q1...qn-1qn
b) On considère que la suite définie par Qn=q0q1...qn-1qn. Montrer que la suite Qn est décroissante et convergente vers un réel a tel que 0<=a<1
c)Montrer que sumP(Gk), k=1:n=1-Qn et en déduire que si a est non nul le jeu a une probabilité non nulle de ne jamais se terminer
si a=0 le jeu se termine avec la probabilité 1.
d) On suppose qu'il existe un réel p tel que pour tout n pn=p et soit q=1-p Donner la limire de la suite Qn et en déduire que le jeu se termine avec la probabilité 1.
e) On suppose que pour tout entier pn=1/(n+1). Déterminer Qn et sa limite. Le jeu peut il ne pas se terminer.
f) On suppose que pour tout entier qn=1/(n+1). Déterminer Qn et sa limite. le jeu peut il ne pas se terminer?
g) On suppose que pour tout entier qn=e(-1/(n(n+1)). Déterminer Qn et sa limite. Déterminer la probabilité que le jeu ne se termine pas.

Merci par avance

Posté par margotte (invité)re : Proba 12-11-05 à 14:07

y a t'il quelqu'un qui puisse m'aider?

Posté par
franzre : Proba 12-11-05 à 15:53

Pour la question I a)

On cherche à démontrer pour k\in {4,5,6}\; P_{_{[S1=k]}}[S2=k]=(k-1)/36

Prenons par exemple le cas k=6.
On a 5 possibilités de faire 6 avec 2 dés :
          \array{c100|c100$de\; n^\circ 1 & de\; n^\circ 2\\ \hline 1& 5 \\2 & 4 \\ 3 & 3 \\ 4 & 2 \\ 5 & 1 }

On a donc une probablilté de \frac 5 {36} de faire 6 avec 2 dés.
Pour gagner au 2° coup sachant qu'on a fait un 6 au 1° coup, il faut refaire un 6 donc

P_{_{[S1=6]}}[S2=6]=5/36

(idem pour k=4 et k=5)

Posté par
franzre : Proba 12-11-05 à 16:25

J'ai une suite à cet exercice que je n'arrive pas à résoudre pouvez vous m'aider?
Meme notation qu'en deuxième partie. On suppose maintenant qu'il y a une infinité de joueurs ainsi un joueur qui n'a pas gagné à son tour est définitivement éliminé et la main ne lui revient plus
on pose q0=1
a) montrer que dans ce cas le jeu ne peut être équitable et que pour tout entier on a :
P(Gn)=q0q1...qn-1pn=q0q1...qn-1-q0q1...qn-1qn



Pour la suite de ton exo

le n° joueur gagne si le n-1° perd (c'est à dire que la main arrive au n° jeuer) et que la n° partie conduit à un succès.
p(G_n)=p(\bar {G_1}\cap\bar {G_1}\cap\cdots\cap\bar {G_{n-1}}\cap G_n) = q_1.q_2.\cdots .q_{n-1}.{\large p_n} = q_1.q_2.\cdots .q_{n-1}.{\large (1-q_n)}

(q_0=1 n'est là que pour généraliser la formule)

Posté par
franzre : Proba 12-11-05 à 16:29


b) On considère que la suite définie par Qn=q0q1...qn-1qn. Montrer que la suite Qn est décroissante et convergente vers un réel a tel que 0<=a<1

Q_{n-1}-Q_n=q_0q_1\cdots q_{n-1}\,(1-q_n)

tous les q_i sont compris entre 0 et 1 donc Q_{n-1}-Q_n\ge 0

La suite (Q_n) est décroissante minorée par 0 donc converge vers un réel a\in[0,1]

Posté par
franzre : Proba 12-11-05 à 16:57

c)Montrer que sumP(Gk), k=1:n=1-Qn et en déduire que si a est non nul le jeu a une probabilité non nulle de ne jamais se terminer
si a=0 le jeu se termine avec la probabilité 1.


c'est la conséquence des définitions.



d) On suppose qu'il existe un réel p tel que pour tout n pn=p et soit q=1-p Donner la limire de la suite Qn et en déduire que le jeu se termine avec la probabilité 1.

on est en présence d'une sorte de loi géométrique.


e) On suppose que pour tout entier pn=1/(n+1). Déterminer Qn et sa limite. Le jeu peut il ne pas se terminer.


q_n=1-\frac 1 {n+1}=\frac n {n+1}

Donc           Q_n=\frac 1 2 \, \frac 2 3 \, \frac 3 4 \cdots \, \frac n{n+1}=\frac 1 {n+1}\;\relstack{\longrightarrow}{n\to infty}0

La probabilité que le jeu ne se termine pas est nulle.



Posté par
franzre : Proba 12-11-05 à 17:08

f) On suppose que pour tout entier qn=1/(n+1). Déterminer Qn et sa limite. le jeu peut il ne pas se terminer?

Q_n=\frac 1 {(n+1)!} \;\relstack{\longrightarrow}{n\to \infty} 0


g) On suppose que pour tout entier qn=e(-1/(n(n+1)). Déterminer Qn et sa limite. Déterminer la probabilité que le jeu ne se termine pas.


On a \forall n \in {\mathbb N}^* \;\; \frac 1 {n(n+1)} = \frac 1 n - \frac 1 {n+1} donc

q_n=e^{-\frac 1 {n(n+1)}} = e^{\frac 1 {n+1}-\frac 1 n}=\frac {e^{\frac 1 {n+1}}}{e^{\frac 1 n}}

Q_n=\frac {e^{\frac 1 2}}{e^{\frac 1 1}}\,\frac {e^{\frac 1 3}}{e^{\frac 1 2}}\,\cdots\,\frac {e^{\frac 1 {n+1}}}{e^{\frac 1 n}} = \frac {e^{\frac 1 {n+1}}}{e^{\frac 1 1}} \;\relstack{\longrightarrow}{n\to \infty} \frac 1 e = e^{-1}

Le jeu ne se termine pas avec une probablilté de e^{-1}

Posté par margotte (invité)re : Proba 12-11-05 à 20:01

merci beaucoup, je vais étudier ces réponses mais par contre je reste toujours bloqué pour I c) et I d).
PS: dans tout l'exo tu commences par q1 au lieu de q0 j'ai donc changé ton q1 en q0 et ton q2 en q1 ai je droit de le faire? mon problème est qu'en question III b) je ne comprends pas ta récurrence avec la réponse qu'on attend.
Merci encore

Posté par margotte (invité)re : Proba 12-11-05 à 20:36

je viens d'étudier tes réponses. Par contre pour cette dernière partie je ne vois pas comment répondre aux questions c) et d) c'est pas si simple pour moi.

Posté par
franzre : Proba 12-11-05 à 23:11

Non tu n'as pas le droit de changer q1 en q0.

Pour que le k° joueur prenne la main, il faut que le k-1° ait perdu.

Or pour le 1° joueur, il n'existe pas de joueur précédent. Pour contourner cet inconvénient, le rédacteur de l'énoncé suppose qu'il existe un joueur n°0 qui perd systématiquement (q0=1). Cela permet d'avoir une écriture générale pour tous les joueurs y compris le 1°.

Bonne soirée

Posté par
franzre : Proba 12-11-05 à 23:12

P.S. : (multiplier par q0(=1 )ne change aucun résultat.

Posté par margotte (invité)re : Proba 13-11-05 à 11:10

merci beaucoup pour cette petite explication, par contre je reste bloquée pour I c) et d) et dans la dernière partie question c et d comment fait on?
merci


Rechercher
Menu
Espace membre
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1732 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !