Inscription / Connexion Nouveau Sujet
Je ne comprend pas pourquoi j'ai faux pour 6/9. ==> tu comprendras plus loin ta confusion (on ne peut pas faire la somme)
ET on a 4/8 de faire plus de 5 si on a 4 au premier. ==> oui
Et on a 9/8 de faire n'importe quel chiffre. ==> tu es bien sûr ? 9/8>1
Je ne suis pas sur en effet mais vous m'avez demandé, au second tirage, combien il y avait de chance de tomber sur n'importe quel nombre. Et il y a 5/8 et 4/8 donc...9/8.
Non, non , non.
Si je fais 5,6,7,8 ou 9 au premier tirage, peu importe le chiffre qui sortira au second tirage, j'aurais au moins 46 euros.
La probabilité de faire 5,6,7,8 ou 9 au premier tirage est de 5/9 (il y a 9 boules en tout).
La probabilité de faire n'importe quel chiffre au second tirage est de 8/8 (il y a 8 boules en tout).
Donc la probabilité de faire plus de 46 euros si j'ai fait au moins 5 au premier tirage est de (5/9)*(8/8)=(5/9)*1=5/9
Si je fait 4 au premier tirage, tout dépendra donc du second, car il faudra que je fasse 6,7,8 ou 9 pour avoir au moins 46 euros à la fin.
La probabilité de faire 4 au premier tirage est de 1/9 (il y a 9 boules en tout).
La probabilité de faire 6,7,8 ou 9 au second tirage est de 4/8 (il y a 8 boules en tout).
Donc la probabilité de faire plus de 46 euros si j'ai fait 4 au premier tirage est de (1/9)*(4/8)=(1/9)*(1/2)=1/18
Donc :
Bonjour,Jedoniezh
je me permets de te signaler une erreur sur ton arbre de 22-05-16 à 17:2
sur les branches des unités lorsque D=4
pour U≤5 p=4/8 =1/2 ( 1;2;3 et5)
pour U> 5 p=4/8=1/2 (6;7;8;et 9)
Bonjour Labo,
Je te remercie, je suis justement en train d'essayer de recouper mon résultat et je n'y arrivais pas.
Une autre façon de le voir (une fois l'exercice terminé)...
Tirages possibles : 9 * 8 = 72
- 12 13 14 15 16 17 18 19
21 - 23 24 25 26 27 28 29
31 32 - 34 35 36 37 38 39
41 42 43 - 45 46 47 48 49
51 52 53 54 - 56 57 58 59
61 62 63 64 65 - 67 68 69
71 72 73 74 75 76 - 78 79
81 82 83 84 85 86 87 - 89
91 92 93 94 95 96 97 98 -
En rouge ceux inférieurs à 46 : il y en a 3 * 8 + 4 = 28
En bleu ceux au moins égaux à 46 : il y en a 72 - 28 = 44
Donc P(S au moins égale à 46) = 44 / 72 = 11 / 18
Bonjour,Jedoniezh
je me permets de te signaler une erreur sur ton arbre de 22-05-16 à 17:2
sur les branches des unités lorsque D=4
pour U≤5 p=4/8 =1/2 ( 1;2;3 et5)
pour U> 5 p=4/8=1/2 (6;7;8;et 9)
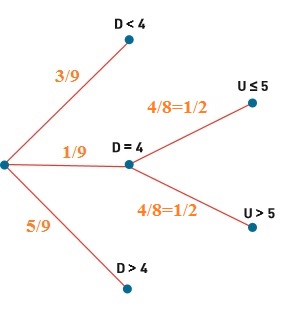
Avec la méthode demandée par l'énoncé :
P(S<46) = P(D<4) + P(D=4 et U<6)
= 3/9 + P(D=4) * P(U<6 sachant D = 4)
= 1/3 + (1/9) * P(U = 1 ou 2 ou 3 ou 5 sachant D = 4)
= 1/3 + 1/9 * 4/8
= 6/18 + 1/18
= 7/18
Et donc P(S au moins égal à 46) = 1 - 7/18 = 11/18
@Lashar
Une fois que tu auras digéré tout cela, sache qu'une autre façon de faire était encore possible, et peut-être même préférable.
On te dit la probabilité de faire au moins 46 euros.
Cette probabilité est donc le contraire de faire moins de 46 euros, donc p(gain>=46)=1-p(gain<46).
La probabilité de de faire moins de 46 euros correspond à :
Faire 1,2 ou 3 au premier tirage (et n'importe quel chiffre au second)==> 3/9
Faire 4 au premier tirage et faire 1,2,3 ou 5 au second tirage ==> (1/9)*(4/8)=1/18
d'où p(gain<46)=(3/9)+(1/18)=7/18
Donc p(gain>=46)=1-p(gain<46)=1-(7/18)=11/18
on retrouve bien le résultat de 18:41
L'arbre de Jedoniezh...
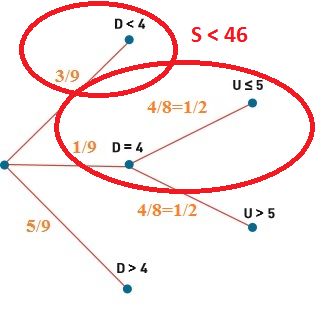
... et le calcul qui va avec :
P(S < 46) = P(D<4) + P(D=4 et U<6)
= 3/9 + 1/9 * 4/8
= 6/18 + 1/18
= 7/18
P(S >= 46) = 1 - 7/18 = 11/18
Pour aller dans le sens de Jedoniezh : quand il y a plusieurs méthodes de calcul, c'est bien de les essayer toutes pour les comparer et consolider sa compréhension du problème.
Bonjour LeDino, merci de ton (tes) intervention(s) à si bon escient.
@Lashar, à mon sens, cet exercice me semble d'un plutôt bon niveau pour un exercice de seconde, je pense qu'il doit être classé dans les exercices difficiles (au moins).
traitement d'image (je fais tout avec ça depuis très longtemps, même qd je travaillais, ici qd je modifie les images sur le site, idem, .... c'est un logiciel libre, de mémoire, il tourne aussi avec windows)







