Annuler
connectez vous
probabilités en post-bac
- Un best-of d'exos de probabilités (après le bac)
- Équations différentielles : un Cours complet avec des exemples
- Ensemble et application Partie II
- Généralités sur les matrices, applications linéaires, changement de base, rang d'une matrice - supérieur
- Espaces vectoriels et Applications linéaires - supérieur
- Ensemble et application Partie I
Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques SupérieurOn parle exclusivement de maths, pour le supérieur principalement, les BTS, IUT, prépas... Licence Maths 1e ann ProbabilitésTopics traitant de probabilités [tout]Lister tous les topics de mathématiques
Niveau Licence Maths 1e ann
Probabilités conditionnelles
Posté par Lau1
Bonjour,
Je dois résoudre l'exercice suivant :
" Une lettre a la probabilité p de se trouver dans un bureau; ce bureau a 2 tiroirs disjoints T1 et T2.
On range 3 fois plus de lettre dans T1 que dans T2.
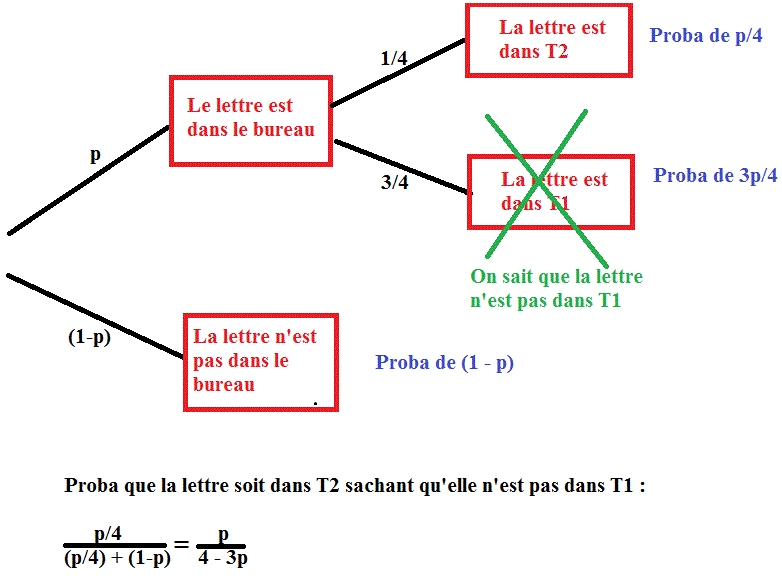
La probabilité que la lettre se trouve dans T2 sachant qu'on ne l'a pas trouvée dans T1 vaut?"
Je n'arrive pas à comprendre la solution : p/(4-3p).
En vous remerciant de votre aide.
Bonsoir,
je note l'événement « la lettre arrive dans ce bureau »,
elle est dans le tiroir T1 et
de même.
L'énoncé donne et
On a donc et
On veut calculer
Comme et
sont incompatibles on a
D'où