Inscription / Connexion Nouveau Sujet
problème à résoudre avec fonction
bonjour, je suis au dernier exercice et besoin d'aide s'il vous plait . Je recopie l'exercice 2 .
Un détaillant vend des calculatrices ,il a remarqué que :
-au prix de 43€ la calculatrice, il en vend 29
-à chaque fois qu'il baisse le prix d'une calculatrice de 1€,il en vend une de plus
Le but de l'exercice est de déterminer le prix d'une calculatrice permettant la recette maximale.
1) Qu'elle est la recette lorsque le prix d'une calculette est de 39€ ?
2)Soit x le montant de la réduction sur le prix d'une calculatrice .
Exprimer en fonction de x :
a)le prix d'une calculatrice.
b)le nombres de calculatrices vendues
c)la recette,notée R(x)
3)Montrer que R(x) = 1296 - ( x - 7)²
4)compléter le tableau de valeurs suivant :
x / 0 / 1 / 2 / 3 / 4 / 5 / 6 / 7 / 8 / 9 / 10 / 11 / 12 /
R(x)/1247/1260/1271/1280/1287/1292/1295/1296/1295/1292/1287/1280/1271/
5)Tracer,sur papier millimétré,la courbe représentative de la fonction R dans un repère orthogonal de votre choix.
6)Par lecture graphique,déterminer la recette maximale. Quel est le prix d'une calculatrice ? Combien en vend t-il ?
pour 1) j'ai fait :
prix / calculatrice/ recette
43€ x 29 = 1247€
42 x 30 = 1260
41 x 31 = 1271
40 x 32 = 1280
39 x 33 = 1287
38 x 34 = 1292
37 x 35 = 1295
36 x 36 = 1296
35 x 37 = 1295
34 x 38 = 1292
33 x 39 = 1287
32 x 40 = 1280
31 x 41 = 1271
30 x 42 = 1260
la recette est de 1287€ lorsque le prix d'une calculatrice est à 39€
la question 2 ,serait mon petit tableau ci-dessus . ???
Non parce que l'on ne va pas s'amuser à faire toutes les valeurs
on part de 43 et on baisse de le nouveau prix est donc
on vend au départ 29 et on ajoute donc calculatrices puisque l'on a baissé de
Quel est alors le nombre de calculatrices vendues ?
Quelle est alors la recette ?
On vous a aidé en posant toutes les questions
à chaque fois j'ai enlevé 1€ au pris de 43 et j'ai ajouté 1 calculatrice .
A la recette maximale j'ai enlevé 7 et ajouté 7 calculatrices
(43-7) (29+7) = 1296 de recette
j'ai regardé le cours mais je n'ai pas appris la forme canonique .
oui j'ai appliqué cette formule ,pour remplir le tableau de l'énoncé . Je vois pas trop ce qu'il faut inscrire à la question 2 ou ce ne sont que des infos pour la suite de l'exercice ?
Oui ça je l'avais fait
R(x)= 1296-(x-7)²
R(x)= 1296- (43-7)²
R(x)= 1296- 36²
R(x)= 0
Par contre pour les autres je ne retrouve pas zéro
vous avez une identité remarquable vous pouvez bien la développer.
Pour déterminer on étudiera la fonction Ou si vous n'avez jamais étudié de fonction second degré pour quelle valeur de
est-il maximal ?
je ne vois pas comment développer
oui c'est la recette maximale mais je le vois d'après le tableau que j'ai développé par tatonnement ,comme vous dites et j'en suis conscient .
bonjour, j'avais pigé qu'il fallait l'utiliser mais mes parents m'ont ordonné de me coucher…
R(x)=1296-(x-7)²
=1296-x²-2x X 7+7²
=1296 - x² -14x+49
et voilà je me suis précipité ..
R(x)=1296-(x-7)²
=1296 -( x²-2x X 7+7²)
=1296 -(x²- 14x + 49 )
=1296 -x² + 14x -49
=1296 -49 -x² +14x
=1247 -x² +14x ICI je retrouve la recette du prix de départ > 1247
R(x)=(43-x)(29+x)
=(43-7)(29+7)
= 36 X 36
= 1296 Hum , cette equation fonctionne bien
je ne retrouve pas la même chose !
R(x) =1247 -x² +14x Je vais remplacer le x par 7 suivant le tableau
=1247-7²+14X7
=1247-49+98
=1296
Et par la magie des maths > c'est identique
J'en conclue quoi du coup, que ces deux fonctions sont identiques ?
Le 7 n'a aucun intérêt ici. Ce n'est pas parce que vous l'avez deviné qu'il faut le mettre partout.
Avez-vous déjà résolu des équations ? ou manipulé des expressions algébriques ?
Pour l'instant vous ne pouvez pas dire que c'est . On a seulement
Calculons maintenant .
Par conséquent
À quelle condition est-il maximal ?
et
sont des réels positifs.
sera maximal si l'on enlève rien à 1296 c'est-à-dire si
Il en résulte que
À quoi ?
Le maximum est 1296 obtenu pour c'est-à-dire lorsqu'il vendra
calculatrices à
euros.
Ce résultat, on vous demande de l'obtenir par lecture graphique objet des dernières questions.
d'accord je vais maintenant regarder pour faire ce graphique . Je ne sais pas si ce sera possible de le poster ?
il vendra 36 calculatrices à 36€
Je vais faire le graphique un peu plus tard et tracer la courbe .Merci, à tout à l'heure si vous êtes disponible
bonjour Mr Hekla .
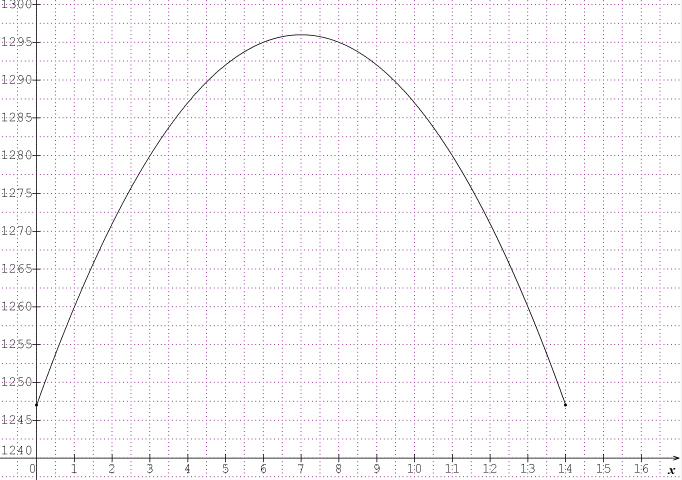
bien lu le 5) de la faq ,j'essaye de mettre le graphique .On voit bien la recette principale 1296 et sur la ligne des abscisses 7 .Donc 43-7=36.
En changeant un peu les échelles et en commençant sur l'axe des ordonnées à 1240
Le maximum est bien obtenu pour