Inscription / Connexion Nouveau Sujet
problème avec fonctions
Bonjour, j'ai un Dm de Maths (Niveau Seconde) à rendre très prochainement.
J'aurais besoin de votre aide s'il vous plaît, je suis vraiment perdue.
Voici le problème suivant :
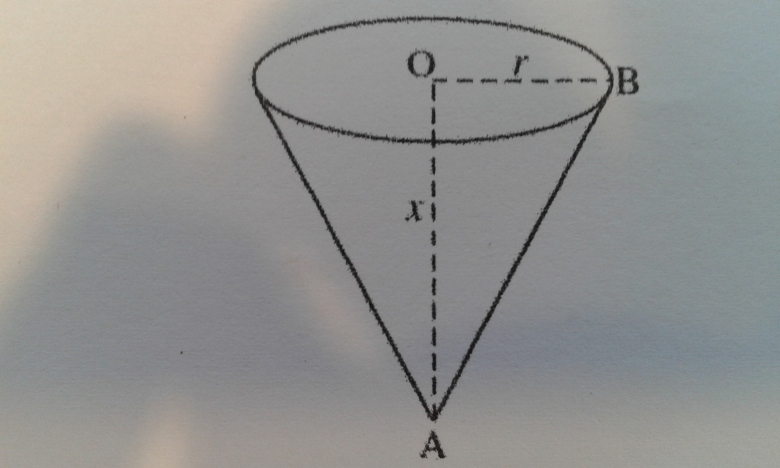
On veut former un cornet de cacahuètes en forme de cône à partir d'un disque en carton de 8cm de rayon.
[deux images illustrent ce cornet]
On appelle f la fonction qui est à la hauteur x du cornet fait correspondre son volume.
1- Déterminer le domaine de définition Df.
2- Exprimer r en fonction de x.
3- En déduire que pour tout x de Df, on a : f(x)= π/3(- x au cube + 64 x)
4- On décide que le cornet doit avoir un volume de 125 cm cube.
Résoudre l'équation nécessaire puis conclure sachant que l'on souhaite également que le cornet soit suffisamment pointu pour bien tenir en main.(Donner une valeur approchée de la solution retenue au mm près).
Pour la question 1, j'ai répondu que le domaine de définition de Df est AOB. Mais je ne suis absolument pas sûre.
Pour la question 2, j'ai tenté diverses calculs, je suis arrivée finalement à
(π*64*x)/3 . J'ai trouvé ce calcul avec la formule du volume qu'on nous donne en bonus mais ça ne semble pas correct non plus.
Pour la question 3, je suppose qu'elle est en lien avec la question 2 donc j'ai passée cette question.
Pour la question 4, je n'ai pas vraiment d'idée pour résoudre cette équation vu que je n'ai pas les calculs nécessaires.
Relis bien l'énoncé, f est une fonction qui à la hauteur x fait correspondre le volume du cornet (c'est à dire volume du cône )
Dis peux tu exprimer le volume du cône en fonction de la hauteur x... vas y
Non mais sans blague !! Df C'est l'ensemble de définition !!!! Et vu la forme de ta fonction , quelle est la nature de ta fonction f ?
Oups
Df= [x;r] ?
(J'ai vu en cours l'ensemble de définition avec une courbe, et on avait noté [6;22] 6 c'était où la courbe démarrait et 22 la fin de la courbe) Est-ce cela ??
Non mais sans blague !! Df C'est l'ensemble de définition !!!! Et vu la forme de ta fonction , quelle est la nature de ta fonction f ?
Tu réponds à ma question ou tu préfère aller dans tout les sens ?

En s'en fiche alors , du coup on a affaire à une fonction affine , par conséquent quel serait son ensemble de définition ?
Pour plus de rigueur en fait sinon f est linéaire, mais qui est une particularité de fonction affine , sinon linéaire c'est plis rigoureux ... bref 
Son ensemble de définition serait Df= [x;r] ?
enfin je ne sais pas si c'est cela mais je sais que ce sont x et r qui sont concernés non ?
C'est  son ensemble de définition il faut relire ton cours !! Les fonctions affines et linéaires sont définies sur
son ensemble de définition il faut relire ton cours !! Les fonctions affines et linéaires sont définies sur 
Ah mais oui, je l'ai vu ça ! Mais je pensais pas que c'était cela qu'il fallait dire.
Merci de votre aide 
Bah c'est sûr que quand on est préoccupé à rapidement aboutir à la réponse, et que on n'oublie de prendre la peine de bien lire et de savoir ce que l'énoncé demande réellement c'est compliqué !!
Bref ... Et pour la question 2) ??
f(x)= π *r au carré ?
Je vous remercie mais je vais faire une pause pour aujourd'hui, je reprends demain.
Merci
Bonne soirée
Considére le triangle ABO rectangle en 0 , tu applique Pythagore ...
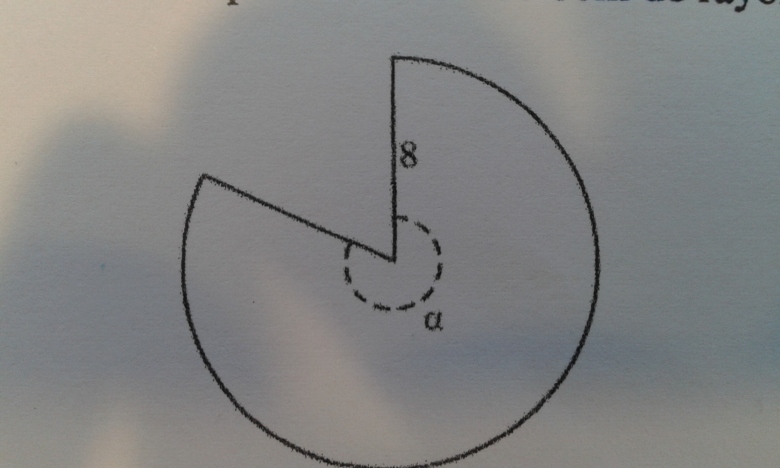
Dans la fig2 c'est une rotation d'angle alpha de ton cornet il suffit d'imaginer que tu tiens ton cornet par le bout pointu(point A) tu le fait tourner sur lui même (rotation dangle alpha ) ca decrira un cercle dont le rayon est R= AB =8cm...
D'accord, j'ai donc essayé avec le Théorème de Pythagore mais je trouve 0, c'est normal ?
J'ai du encore faire une bêtise 
J'ai noté ça :
AB²= AO²+OB²
8²= AO²+ 8²
AO²= 8²-8²
AO²= racine de 0
AO= 0
Parceque justement tu prends pas la peine de lire correctement ce que j'écris ou les piste que je te propose
Tu fais mine de bien comprendre tandis que c'est la réponse qui timporte ...
Relis (post 12h 19 et post 15h13)
C'est la même chose que :
(sauf que dans l'expression précédente , j'ai juste réécris ça de manière plus élégante
 et surtout pour bien voir qu'on a exprimé en fonction de x
et surtout pour bien voir qu'on a exprimé en fonction de x