Qu'as-tu essayé ? As-tu écrit les équations des tangentes ?

J'ai pris les coordonnées du milieu du segment [H1F] et [H2F], avec H1 et H2 projetés orthogonaux de M1 et M2. Puis j'ai établi l'équation de la droite d1 passant par le milieu de [H1F] et M1, puis celle de la droite d2 passant par le milieu de [H2F] et M2.
Ensuite, j'ai posé d1=d2.

Sur la directrice (D)
Peut-être avec y=f(a)+f'(a)(x-a) ?
Non je ne tombe pas sur le résultat demandé avec ma méthode, car chez moi le paramètre p s'annule dans les coordonnées des points, donc il ne reste plus de p pour la suite des calculs, alors qu'il est censé y en avoir au final.

Pour la version matricielle, on ne l'a pas encore vue en cours, donc je préfère mettre autre chose.

En utilisant ta méthode, je trouve naturellement deux équations de droites telles que:
d₁: (x-x₁)(y₁²-2p)+(y-y₁)(2y₁-2px₁)=0
d₂: (x-x₂)(y₂²-2p)+(y-y₂)(2y₂-2px₂)=0
Et après, qu'est-ce que je peux faire avec elles ? d₁=d₂ ?

Tu as une drôle de façon de calculer les dérivées partielles ! C'est faux.

N'emploie "ma" méthode que si ça fait partie des résultats que tu as vu en cours ! Est-ce le cas ?

Il reste la possibilité de calculer la tangente pour .

Ben en fait on n'a pas vraiment vu de méthode pour calculer cela en cours, je ne sais pas du tout comment commencer du coup.
Pour x=g(y): il faudrait alors écrire l'équation telle que x=y²/2p ?

Tu ne réponds pas franchement : le résultat que je cite sur l'équation de la tangente d'une courbe implicite fait-il ou ne fait-il pas partie de tes cours ?

Ensuite, , c'est effectivement l'équation de la parabole. Et calculer la tangente au graphe d'une fonction, tu dois savoir faire, n'est-ce pas ? (Tu l'as même écrit plus haut). Ce n'est pas le fait qu'ici est le nom de la variable et le nom de l'image par la fonction qui doit t'arrêter.

Non, ce résultat-là ne fait partie de mes cours.

Ici, en utilisant la formule de la tangente, je trouve:
d₁: x=(y₁/p)(y-y₁)+(y₁²/2p)
et d₂: x=(y₂/p)(y-y₂)+(y₂²/2p)

Bien. Il reste à calculer l'intersection de ces deux droites. Tu peux auparavant faire un peu de nettoyage dans les équations.

En posant d₁=d₂, je tombe sur:
(y/p)(y₁-y₂)+(1/2p)(y₂²-y₁²)

"Poser d_1=d_2" au mieux ne veut rien dire.
Ce que tu fais, c'est que tu résous le système formé par les deux équations de droites.
Et la ligne que tu écris ensuite ne comprends pas le signe =
Fais un effort de clarté et de précision dans la rédaction.

Enfin, tu obtiens bien ainsi l'ordonnée de l'intersection des tangentes, n'est-ce pas ? Et après, tu peux facilement avoir l'abscisse.

Oui, désolé pour le =, je ne m'en suis aperçu que trop tard ^^

Et effectivement, j'ai trouvé les coordonnées du point P ! Merci déjà pour cette question !

Je mets la suite:
2) Soit I le milieu du segment [M1,M2] et soit K le milieu du segment [PI]. Montrez que K est un point de la parabole T.

Je pense avoir trouvé les coordonnées du point K:
(x_K , y_K)=((1/4)((y₁y₂)/p+x₁+x₂) , (y₁+y₂)/2)
Mais en remplaçant y par y_K dans l'équation de  parabole, je ne retrouve pas x_K.

Ah, bon, pourquoi ? Aurais-tu oublié que les points et sont sur la parabole ?

Je ne vois pas vraiment ce que tu veux dire par là.

Salut,

Il semble qu'on fasse le même dm. J'ai moi aussi quelque difficulté à résoudre la première question, j'ai d'abord tracer la figure sur geogebra
_{***lafol  image rapatriée sur le serveur de l'île, merci de le faire toi même la prochaine fois}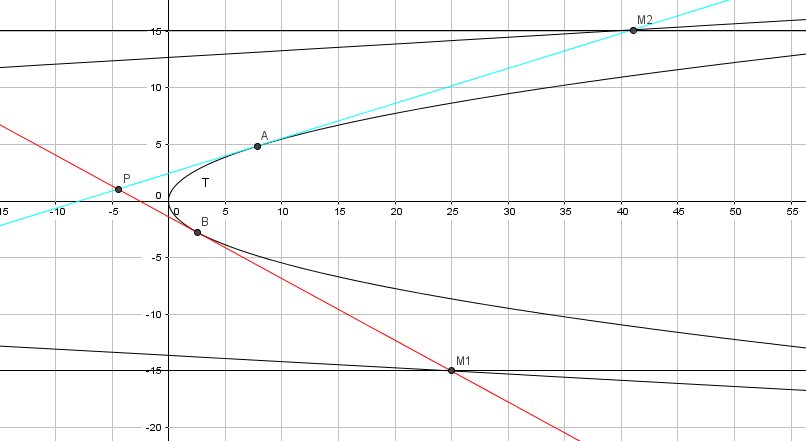

En gros, on veut montrer que les tangentes de la parabole T passant par M1 et M2 (et du coup par les points A et B sur ma figure) s'intersectent au point p de coordonnées

                                             (  (1/(2p)) yM1 yM2  ,  (yM1 + yM2)/2  )

J'ai essayé de trouver l'équation des tangentes en procédant comme cela;

y²=2px
y=sqrt(2px)
y=f(x)
y=f''a)(x-a)+f(a)
f'(a)=(sqrt(2pa))'= ((2pa)')/(2sqrt(2pa)) = (2p)/(2sqrt(2pa))
y= (2p) / (2sqrt(2pa)) * (x-a)+ sqrt(2pa)
y=(2px-2pa)/(2sqrt(2pa)) + sqrt(2pa)

Après j'ai essayé pleins de simplification sans jamais arrivé à rien...
Ensuite je ne comprend pas trop comment procéder avec cette méthode. On trouve l'équation d'une tangente, mais pour la seconde tangente on aura necessairement la meme mais avec un a' non ?

Quand tu calcules , que trouves-tu ? Ce n'est pas nul ?

Je trouve (y1+y2)²-2p(x1+x2)-2y1y2=0.

Donc tu trouves bien que c'est nul, c'est ce que tu as écrit, n'est-ce pas ?

Oui, c'est bien ce que j'ai écrit, mais qu'est-ce que l'on peut conclure avec cela ?

edit: d'accord en relisant vos derniers post je vient de comprendre que la phrase "M1 et M2 deux point disctincts de T" signifie que les 2 points sont distincts entre eux, et non pas distinct de la parabole...

Bonjour
Il y a quand même moins de calculs quand on permute les axes
X=y
Y=x
Y=X²/(2p)
Y'=X/p
On arrive par exemple à X(P)=(X1+X2)/2  soit y(P)=(y1+y2)/2

Bonne remarque, pondy; tu aurais juste peut-être pu lire le fil, tu aurais vu qu'elle avait déjà été faite et employée.

Oui, je suis d'accord. Mais je pense qu'on s'est mal compris.
En fait, quand j'ai écrit "(y1+y2)²-2p(x1+x2)-2y1y2=0", je suis parti au départ de y²=2px. Donc le 0 était toujours là. En simplifiant l'équation entre guillemets, je tombe sur (y1+y2)²=2p(x1+x2). On voit que l'équation ressemble à celle de la parabole, telle que
y=y1+y2
et x=x1+x2.

On s'est mal compris parce que tu t'es mal exprimé. Moi, je prends au pied de la lettre ce que tu écris. Je ne vais pas me dire que peut-être ce que tu penses n'est pas ce que tu écris ! (Je te signale d'ailleurs que dans une copie d'examen, ce qui est jugé est ce que tu écris pour de vrai, pas ce que tu penses avoir écrit).

Peux-tu m'expliquer comment tu passes de (y1+y2)²-2p(x1+x2)-2y1y2 à (y1+y2)²-2p(x1+x2) ?

Et une nouvelle fois, tu as oublié que et sont sur la parabole, c.-à-d. que et vérifient l'équation de la parabole.

Noreply: En partant de (y/p)(y1-y2)+(1/2p)(y2²-y1²)=0, isole y et après ça va tout seul Tu trouveras le y qu'il faut, puis tu pourras l'utiliser pour dans l'équation de la parabole pour enfin trouver x.

Recomic: je fais des fautes très bêtes aujourd'hui. Une supplémentaire: je trouve y1²+y2²-2p(x1+x2) et non pas (y1+y2)²-2p(x1+x2).

Conclusion ?

TotoLebeau67,
la où je décroche c'est avant d'arriver a ce résultat.
en posant x = y² /2p et en utilisant f'(a)(x-a)+f(a),
j'arrive à x = (2ay-a²) / 2p.

Ce qui, en le réinjectant dans l'équation de départ, me donne

y² = 2px
      = 2p * ( (2ay-a²) / 2p )
      = 2ay-a²
cad 2ay-a²-y² = 0

Et je n'ai plus de p dans mon équation !

(y1²-2px1)+(y2²-2px2)=0
Et donc, comme (x1,y1) et (x2,y2) vérifient l'équation de la parabole, on peut en conclure que K est un point de T.

Noreply: Il faut que tu écrives deux équations de tangentes: en M1, et en M2. Et remplace les a par y1 ou y2, ça dépend de quelle tangente on parle. Puis tu devras résoudre l'équation d1=d2 en remplaçant par chacune des équations de tangente trouvée.

Allez, encore un p'tit effort, Noreply !

Autant pour moi Noreply, je n'avais pas cerné à quelle moment du calcul tu étais. En fait, t'isoles y. Et tu peux utiliser une identité remarquable pour  (y2²-y1²).

"d1: x=...
et d2: x=...
Donc tu prends ...=... "

Mais c'est ce que je fais depuis le début !

Du coup j'ai persevere dans cette vois;
| -y² +2 y1 y - y1² =0
| -y² +2 y2 y - y2² =0

Après en posant l'égalité je débouche sur
2 (y1 y-y2 y)-y1²+y2² =

(avec des a et b c'est plus lisibles, donc on a
2(ay-by)-a²+b²=0
2y(a-b)-a²+b²=0
2y(a-b)=a²-b²
y=(a²-b²)/(2(a-b))

Et la j'arrive plus à simplifier !
J'ai alors essayé de réinjecter dans l'équation de la parabole mais j'obtiens des trucs horribles!

J'ai peux être des problèmes de calculs, je ne vois pas comment aller plus loin...

hmmm...

Bon je ne vois pas pourquoi mais en posant sur ma calculette je trouve bien que

(a²-b²)/(2(a-b)) est égal à (1/2)(a+b)

Si quelqu'un pouvait m'expliquer d'où ça vient... je n'ai rien trouvais sur le net

(   (a²-b²) =/= (a-b)²   je ne vois pas pourquoi  a*a - b*b / (a+b) donne a + b   )

Ben dis donc, sacrées lacunes sur les identités algébriques !
Il ne te viendrait pas à l'idée de calculer (a+b)(a-b) ?

Pourquoi réinjecter dans l'équation de la parabole ? Le point d'intersection des deux tangentes n'est sûrement pas sur la parabole, voyons !
Par contre, si tu réinjectes l'ordonnée trouvée dans l'équation d'une des tangentes, tu vas bien trouver l'abscisse du point d'intersection.