up

Salut bncjo

Exprime la derivée n-ième avec lieibniz (la somme doit aller de k=0 à k=2)
après remplace f^n(x) par Pn(x)/((1-x²)^(n-0.5))
fai de meme pour les termes de droite (il doit y avoir du f^n, du f^(n+1) et du f^(n-1))
après tu vires ton ((1-x²)^(n-0.5))

Et a la fin tu doit obtenir une relation entre 3 Pn(x) consecutifs apres c'est a toi de remplacer n par n+1 ou n-1
pour avoir une relation entre les trois termes voulus.

Je n'ai fais aucun calcul mais c'est comme cela qu'il faut faire
Bonne fin de journée

merci denigato mais comment exprimes-tu la dérivée n-ieme avec leibniz?

Désolé je n'avais pas le temps de le reecrire a l'ordi j'espere que l'administrateur acceptera.
Ceci n'est qu'une ébauche, à toi de finir le travail
Bonne nuit

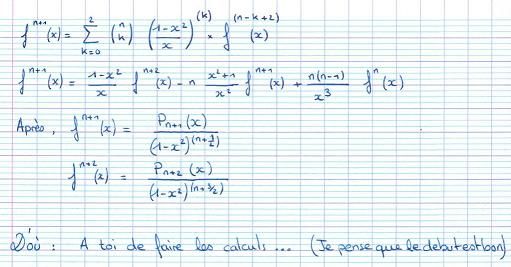
Pourquoi multiplie-t-on par commme deuxième fonction de la formule de Leibniz ?

C'est grace à cette relation. (1-x²)f''(x)-x*f'(x)=0

f '(x) = (1-x²)/x f ''(x)

est-ce que vous pouvez m'envoyer cette question s'il y un document ?
Car je suis etudiant de ECPkn a Pekin,j'ai besoin de faire cette probleme pour preparer l'examen de mi-semestre.
e-mail:***
merci....

_{***lafol > évite de mettre un mail en clair, si tu veux être recontacté, indique le plutôt dans ton profil}

bonjour
tu as "déterré" un "topic-fossile" âgé de plus de huit ans... les intervenants ne fréquentent plus ce forum : tu le vois à la couleur verte de leur pseudo
as-tu des questions précises concernant cet exercice ? tout avait été expliqué par denigato, mais si tu as besoin de compléments, n'hésite pas.