Inscription / Connexion Nouveau Sujet
Problème DM
Bonjour,
Je suis bloqué sur un exercice de mon DM de maths, le sujet est le suivant:
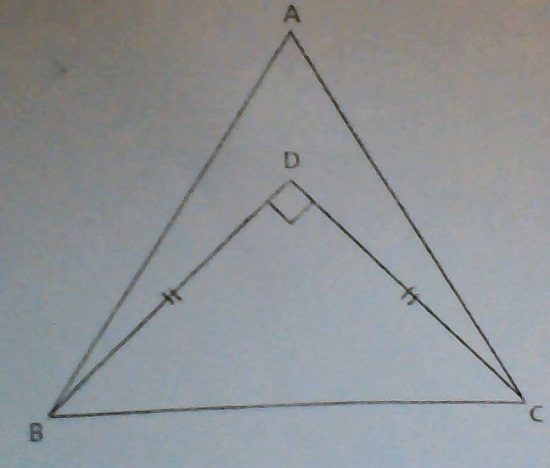
Dans la figure ci-dessous, ABC est un triangle équilatéral de côté 2 et BDC est un triangle rectangle isocèle en D
1) Démontrer que la droite (AD) est perpendiculaire à la droite (BC). On note H leur point d'intersection.
2) Calculer, en degrés, la mesure de l'angle ABD.
3) Soit K le pied de la hauteur issue de D dans le triangle ABD.
Démontrer que: KD = √2 x sin 15°.
4)a. Calculer l'aire du triangle BDC et celle du triangle ABC.
b. En déduire l'aire du triangle ABD.
5) A l'aide des questions 3) 4), établir que: sin 15° = √6 - √2 /4.
6)a. Donner alors la valeur exacte de la longueur KD puis montrer que:
BK= √3 + 1 /2. On vérifiera que 4+ 2√3= (√3+1)².
b. Etablir alors que: cos 15°= √6 + √2 /4.
La figure de l'exercice se trouve ci-dessous.
Je vous pris de bien vouloir m'aider, merci d'avance.
Bonjour,
et qu'as tu fait la dedans ?
les deux premières questions sont "collège"
la question 3 c'est définition du sinus
la question 4 c'est formule d'aire classique
les deux hauteurs se calculent soit par Pythagore, soit par la trigo à partir des tangentes des angles remarquables et connus par coeur 45 et 60°
4b c'est une simple soustraction !
etc ... fais déja ça !!
Bonsoir,
merci de votre réponse,
Pour le 1, j'ai dit que BAC est équilatéral et BDC est isocèle et partagent la même base que BC, (AD) coupe (BC) en son milieu, la hauteur de (BC) coupe (AD) perpendiculairement.
Pour le 2, j'ai trouvé 15°.
Pour le 3, il faut utiliser Pythagore pour trouver √2 (Mais je ne sais pas comment rédiger étant donner que nous avons qu'une seule longueur dans le triangle) puis pour calculer KD on utilise sinus pour arriver à x sin 15°.
Pour le 4, je crois que c'est: Base x hauteur/ 2, donc pour BDC, si on le coupe en 2 alors CH= HD = 2 cm ce qui fait 2cm² pour BDC. Pour ABC, la longueur AH j'ai √3, je n'arrive pas à la calculer...
Pour le 3, il faut utiliser Pythagore pour trouver √2 (Mais je ne sais pas comment rédiger étant donner que nous avons qu'une seule longueur dans le triangle)
c'est pas celui là qui est intéressant c'est BCD pour avoir BD. c'est lui qui fait un truc en racine de 2.
et tu as dit toi même que HB = HD
et ensuite
KD = BD sin(15°) oui (autant appeler x par son nom hein ...)
pour AH c'est encore Pythagore dans AHB (le triangle est équilatéral AB = BC !)
ah non c'est bon j'ai trouvé il fallait travailler sur le triangle DBH...
Par contre est ce que ma réponse de l'exercice 1 est elle bonne svp ?
la rédaction est très bof et en fait non c'est faux (ça ne démontre rien du tout et en plus énonce des trucs faux)
BAC est équilatéral et BDC est isocèle et partagent la même base que BC,
OK sauf la grammaire. la même base "que" BC ne veut rien dire
(AD) coupe (BC) en son milieu,
non c'est une affirmation gratuite.
la hauteur de (BC) coupe (AD) perpendiculairement.
la hauteur d'une droite ???
la rédaction la plus propre à mon avis de cette espèce d'évidence qu'il est plus difficile de rédiger correctement que des trucs moins évidents :
AB = AC donc A appartient à la médiatrice de [BC]
DB = DC donc D appartient à la médiatrice de [BC]
la droite (AD) est donc la médiatrice de [BC] et lui est donc perpendiculaire
et de plus coupe BC en son milieu. H est donc le milieu de BC
merci beaucoup,
donc pour le 4, j'ai réussi à trouver V2 x sin 15°
le 5) a. BDC=1 cm² b. ABC= V3 cm²
b. V3/2 - 1/2 = V3-1/2
Par contre le 6, je n'ai pas trouvé
donc pour le 4, j'ai réussi à trouver V2 x sin 15°
le 5) a. BDC=1 cm² b. ABC= V3 cm²
b. V3/2 - 1/2 = V3-1/2
question 3) Soit K le pied de la hauteur issue de D dans le triangle ABD.
Démontrer que: KD = √2 x sin 15°. fait donc
question 4) a. Calculer l'aire du triangle BDC et celle du triangle ABC. fait OK
b. En déduire l'aire du triangle ABD.
V3/2 - 1/2 OK
= V3-1/2 faux
ce que tu écris là veut très exactement dire
je suppose que tu voulais dire
fait donc, en corrigeant ton écriture qui méprise les parenthèses obligatoires
(lire cours de 5ème
Tu en es donc à la question 5 et pas 6
A l'aide des questions 3) 4), établir que: sin 15° =
exprimes l'aire de ABD de deux manières différentes :
comme (1/2)AB.BK en utilisant BK de la question 3
directement comme résultat de la question 4
elles sont bien sûr égales puisque toutes deux représentent l'aire du même triangle ABD...
D'accord merci
Donc pour l'aire ABD c'est: Aire ABC - Aire ADH ce qui fait (V3 - 1)/2
Pour l'exercice 5 Il faut faire 2 x V2 x Sin 15°, Puis on calcule Sin 15°=(V3-1)/2V2
On obtient donc: (V6-V2)/4
Par contre la dernière question je n'ai pas compris...
pour la question 6 eh bien maintenant que tu as la valeur exacte de sin(15°) = (V6-V2)/4
tu peux calculer la valeur exacte de DK = sin(15°) 2, simplement en remplaçant sin(15°) par cette valeur que tu viens de calculer !
2, simplement en remplaçant sin(15°) par cette valeur que tu viens de calculer !
et ensuite un Pythagore pour calculer BK
l'indice "on vérifiera que" sert à simplifier l'écriture de BK (sinon des racines carrées de racines carrées)
"on vérifiera que" veut dire développer (√3+1)² et ça devrait donner 4+ 2√3 si pas d'erreurs de calcul
et donc la simplification de BK en l'expression annoncée.
et en déduire au final cos(15°) = BK/BD


