Inscription / Connexion Nouveau Sujet
probleme math x
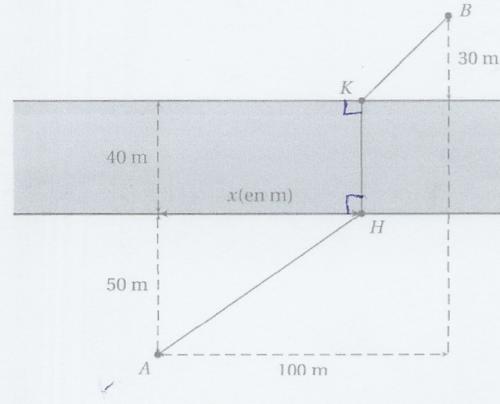
Sujet: L'objectif est de déterminer où placer le pont [HK] perpendiculaire aux berges de la rivière, supposées parallèles, pour que la longueur du trajet de A à B soit la plus petite possible.
fichier math
Il y a deux façons de faire la première est surtout numérique. J'ai trouvé après plusieurs calculs que x doit être égale à 60m pour que le trajet soit le plus court.
Par contre pour la deuxième, l'exercice indique que la méthode est purement géométrique basée sur un réarrangement des trajets pour résoudre ce problème qui est accessible depuis la 4° (Théorème de Thalès nécessaire pour conclure).
Pour le théorème j'ai pensé à la configuration basique où il faudrait supprimer les 40m pour les calculs puis les rajouter à la fin. Mais j'ai beau revoir mes leçons de 4°, me creuser la tête je n'arrive pas à prouver la bonne solution.
Alors si quelqu'un peut au moins ne dire ce que je dois utiliser pour trouver la solution ce serait super !
Merci d'avance.
bonjour,
t'as compris ce que tu as recopié ?
![]()
mathafou ici ![]() Minimum d'une fonction, sans formule a mis des explications
Minimum d'une fonction, sans formule a mis des explications
Le trajet AHKB se compose d'une partie de longueur fixe (HK) et de deux parties de longueur variable (AH et KB) en fonction de la position du point H.
Pour que la longueur totale de ce trajet soit minimale, il faut que la somme des longueurs variables AH et KB soit minimale.
Si l'on imagine la portion HK supprimée, on voit que cela correspond à l'alignement des points A, H/K et B.
Bonjour,
Si l'on imagine la portion HK supprimée, on voit que cela correspond à l'alignement des points A, H/K et B.
ça donne un calcul et une construction faux
mathafou ici
et d'ailleurs ça ne fait pas x = 60m, tes calculs doivent être faux ...
"supprimer" les 40m est effectivement la clé de la solution géométrique, mais en fait on ne les "supprime" pas du tout !
on les déplace ("basée sur un réarrangement des trajets")
transformer le trajet AH + HK + KB en AH + KB + HK par exemple
(ceci fait apparaitre un parallélogramme)
on obtient ainsi une construction purement géométrique (sans aucun calcul) niveau même pas 4ème.
(d'ailleurs suggérée aussi par la fin du premier lien : déplacer le triangle BKM)
ensuite parfaitement pour trouver x à partir de cette construction, ce sera avec Thalès (qui est donc du programme de 3ème)
à condition encore de l'appliquer correctement ce qui ne me semble pas être le cas de la fin du sujet cité


