Inscription / Connexion Nouveau Sujet
Accueil l'île des mathématiques Forum de mathématiquesListe de tous les forums de mathématiques LycéeOn parle exclusivement de maths, niveau lycée. TerminaleForum de terminale Nombres complexesTopics traitant de nombres complexes [tout]Lister tous les topics de mathématiques
Niveau terminale
Partager :

Problème nombres complexes

Posté par
FerreSucre 11-02-21 à 18:13

Bonsoir, cela fait à peu près une heure que je stagne sur un problème qui semble plutôt basique (même si il est classé en exercice difficile) :

Soit un triangle ABC direct, si on trace un triangle équilatéral de chaque coté de ce triangle et que l'on prend le centre de ces 3 triangles équilatérals (P, Q, R), alors PQR est un triangle équilatéral. Démontrez le.

Une idée ? Comme c'est sur les nombres complexes j'ai pas trop envie d'utiliser des coordonnées x,y et je sais pas si ça simplifierai le problème.

Pour moi il faudrait trouver les coordonnées de P, Q , R en fonction de z_a, z_b , z_c puis utiliser |z_p-z_q| = |z_q-z_r|
sauf que je trouve aucun moyen d'exprimer z_q, z_r, z_p en fonction de z_a, z_b , z_c. Une idée ? merci

Posté par
malou Webmasterre : Problème nombres complexes 11-02-21 à 18:33

Bonsoir

à bosser !

Posté par
matheuxmatoure : Problème nombres complexes 11-02-21 à 18:37

bonsoir

si tu veux travailler avec les affixes...

si P est construit à partir du côté [BC] :

z_P = e^{i\dfrac{\pi}{3}}(z_B-z_C)+z_C

(image de B par la rotation de centre C et d'angle /3 )

où interviennent les centres des triangles équilatéraux dans ta question ?

Posté par
carpediemre : Problème nombres complexes 11-02-21 à 18:39

salut

je pose j=e^{i\frac \pi 3} et j* son conjugué

je note a, b, c, p, q, et r les affixes des points A, B, C, P, Q et R

l'affixe du troisième sommet du triangle équilatéral construit avec A et B est d = a + (b - a)j*

l'affixe de P est alors (a + b + d)/3

il suffit de faire la même chose pour les autres ... en étant attentif à prendre j ou j* suivant dans quel sens on tourne ...

Posté par
matheuxmatoure : Problème nombres complexes 11-02-21 à 18:40

ah ok, j'avais pas compris ton énoncé...

matheuxmatou @ 11-02-2021 à 18:37



si A' est construit à partir du côté [BC] tel que A'CB soit équilatéral direct, de centre P :

z_A' = e^{i\dfrac{\pi}{3}}(z_B-z_C)+z_C

(image de B par la rotation de centre C et d'angle /3 )



et

zP = (zA' + zC + zB) / 3

Posté par
FerreSucrere : Problème nombres complexes 11-02-21 à 18:55

Oulaala faut le deviner ça mdr.. on a pas encore vue les formes exponentielles en cours mais je connaissais juste déjà z = re^(io)

AC' = AB, (AB,AC') = \pi/3 \Leftrightarrow (c'-a) = e^{i\pi/3}(b-a)
Idem pour les autres : (b'-c) = e^{i\pi/3}(a-c)
(a'-b) = e^{i\pi/3}(c-b)

Donc a'+b'+c'-a-b-c = 0 \Leftrightarrow a'+b'+c' = a+b+c

J'ai juste recopié le début du corrigé pour avoir une idée de ou débuter x) je connaissais pas trop cette technique de rotation c'est bon à savoir.

Posté par
FerreSucrere : Problème nombres complexes 11-02-21 à 19:26

Ah bah super j'écrivais un message qui a été supprimé...

r = e^{\pi/6i}(b-a) + a
p = e^{\pi/6i}(c-b) + b
q = e^{\pi/6i}(a-c) + c

p+q+r -a-b-c = 0 \Leftrightarrow p+q+r = a+b+c = a'+b'+c'

r = \dfrac{2e^{i\pi/3}(b-a)+3a+b}{4}
p = \dfrac{2e^{i\pi/3}(a-c)+3b+c}{4}
q = \dfrac{2e^{i\pi/3}(c-b)+3c+a}{4}

\dfrac{2e^{i\pi/3}(b-a)-a-4e^{\pi/6}(b-a)+b}{4} = 0
2(b-a)(e^{i\pi/3}-2e^{i\pi/6})-a+b = 0

j'essayais un truc mais ça donnerai quoi si on faisait un système avec ces 3 équations ? (celle de la dernière ligne avec les 2 autres) ? On pourrait conclure ?

Posté par
Panurgere : Problème nombres complexes 12-02-21 à 13:56

Bonjour,

Citation :
Soit un triangle ABC direct, si on trace un triangle équilatéral de chaque coté de ce triangle et que l'on prend le centre de ces 3 triangles équilatérals (P, Q, R), alors PQR est un triangle équilatéral. Démontrez le.

C'est pas très clair.
Je ne vois pas le lien entre prendre le centre de ces 3 triangles (qu'est-ce que cela signifie ?) et le déduction : alors PQR est un triangle équilatéral
Si l'on interprète ton texte  en : construire un triangle équilatéral sur chaque côté du triangle ABC, alors, au moins dans le cas d'un triangle ABC obtus, le triangle PQR est loin d'être équilatéral !
D'où vient cet énoncé ?

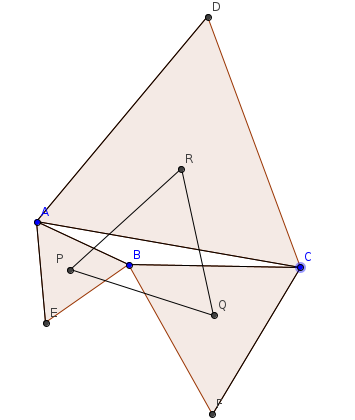
Problème nombres complexes

Posté par
malou Webmasterre : Problème nombres complexes 12-02-21 à 14:07

Bonjour
sur cette figure, P,Q et R sont les sommets des triangles équilatéraux et non pas leurs centres respectifs...

Posté par
Panurgere : Problème nombres complexes 12-02-21 à 14:56

Oui, j'avais corrigé pour ma part.
D'où sort cet exercice qui apparemment est faux ?

Posté par
malou Webmasterre : Problème nombres complexes 12-02-21 à 15:24

ah bon
Problème nombres complexes

Posté par
Panurgere : Problème nombres complexes 12-02-21 à 16:24

Ah mes excuses ! Effectivement j'avais lu de travers !
C'aurait été plus clair ainsi :

Soit un triangle ABC direct, si on trace un triangle équilatéral de chaque coté de ce triangle et que l'on note P, Q, R les centres de ces 3 triangles équilatéraux, alors PQR est un triangle équilatéral. Démontrez le.

J'ai essayé de partir sur les barycentres mais je n'aboutis pas  ...

Posté par
Panurgere : Problème nombres complexes 14-02-21 à 10:37

Je n'étais pas loin du but :

Une c.n.s pour qu'un triangle XYZ d'affixes x, y, z soit équilatéral est que x +jy +j^2z = 0
c'est une propriété un  peu longue à démontrer et je la suppose connuz.

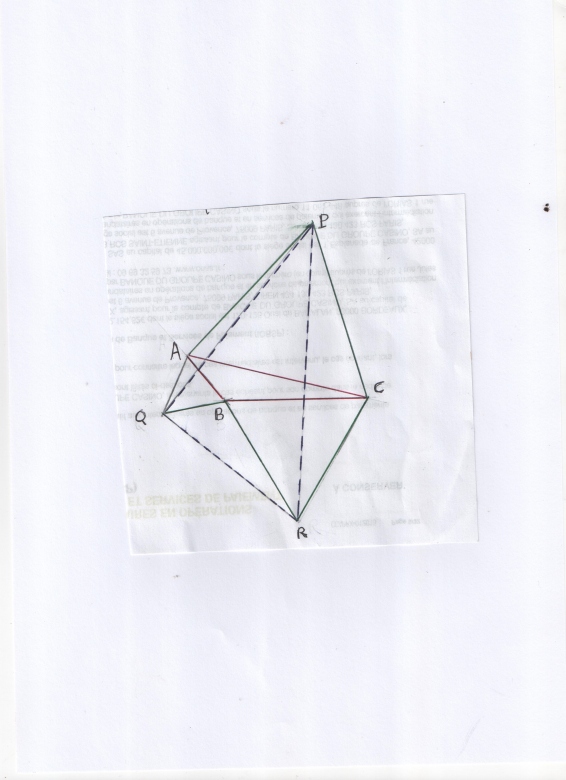
Avec a,b,c d ,e,f p, q, r affixes respectifs de A, B, C, D, E, F, P, Q , R :
P isobarycentre de AEB : 3p = a+b+e (1)
E est l'image de A dans la rotation de centre P et d'angle \frac{2\pi}{3} :
e-p= j(a-p) soit p = p + (a-p)j valeur qu'on porte dans (1)
On aboutit à (1+j)(2 +j)p=(1+j)a+b
1+j+j^2= \frac{1-j^3}{1-j}= 0 d'où 1+j = -j^2
De même pour les triangles isocèles BFC et CDA ;
(2+j) p = -j^2 a+b (2)
(2+j) q =-j^2b+c (3)
(2+j) r = -j^2c+a (4)

(2) + j(3) +j^2(4) donne :
(2+j) (p+jq+j^2r) = -j^2a+b -b +jc -jc+j^2a = 0 car j^3 = 0, j^4=j
p+jq+j^2r=0
Le triangle PQR est équilarétal.


Rechercher
Menu
Espace membre
19 visiteurs
Changer d'île

Vous devez être membre accéder à ce service...

Pas encore inscrit ?

1 compte par personne, multi-compte interdit !

Ou identifiez-vous :

Rester sur la page

Inscription gratuite

Fiches en rapport

parmi 1730 fiches de maths

Désolé, votre version d'Internet Explorer est plus que périmée ! Merci de le mettre à jour ou de télécharger Firefox ou Google Chrome pour utiliser le site. Votre ordinateur vous remerciera !