si tu choisis comme repère (A;AB;AC;AD)
sais-tu donner les coordonnées de A; B; C et D
ensuite on utilise les relations vectorielles pour trouver I, J , K et L

Bonjour,
oui très bien le repère (A;AB;AC;AD)
les coordonnées sont faciles à trouver avec les indications données.
par exemple si AL = AD/4 c'est que L(0;0;1/4)
et quand on ne l'ai a pas directement comme pour BJ=1/4 BC on décompose sur les vecteurs de base avec Chasles
AJ = AB + BJ = AB + (1/4)(BA+AC) =3AB/4 + AC/4 donne J(3/4;1/4;0)

Oui !

A(-1;0;2)
B(3 ; 2 ; -4)
C(1 ; -4 ; 2)
D (5 ; -2 ; 4)
I(1 ; -1 ; 1)
J(5/2 ; 1/2 ; -5/2)
K(3 ; -3 ; 3)
L(1/2; -1/2 ; 5/2)

Merci pour votre réponse, mais pourquoi (0 ; 0 ; 1/4) ...? C'est ce que je cherche à comprendre

Bonsoir ,
Tout est faux  
  petit rappel   dans le plan avec le repère (O,OI, O J)
O(0,0)
I(1,0)
J(0,1)
dans l'espace  avec le repère (A,AB,AC,AD)
A(..,..,..)

Je cherche les points I J K et L pas le point A

Bonjour,

Bonjour,
une autre façon de "voir" ces cordonnées directement :



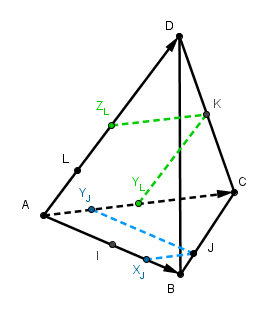
on y "lit" directement les coordonnées de J et de K (au besoin par un Thalès "de tête")
(5/2 > 1 ne tient pas debout cela voudrait dire que ces points sont en dehors du tétraèdre)

PS : et celles de A origine du repère !!

Si tu te trompes sur les coordonnées des points A,B,C,D , tu as peu de chance de trouver ou de comprendre les autres...

Mais les points ABCD je donne ceux qui sont donnés plus haut dans l'énoncé pas ceux que j'ai trouvé, mais pour le repère adapté c'est utile de les calculer?

L'énoncé de 18h10 n'est pas complet ?

Ben je pense pas qu'il y ait besoin des coordonnées de la partie A pour la partie B, je crois que avec les relations BJ = 1/4 BC et AL = 1/4 AD c'est ok non?

@mathafou,
N'aurais-tu pas mis L au lieu de K derrière Z et Y dans la figure ?

Pour J et L j'ai compris par contre pour I et K je bloque encore :/..

N'aurais-tu pas mis L au lieu de K derrière Z et Y dans la figure ?
oui petite erreur de nommage, ça ne change riene au principe

https://www.ilemaths.net/sujet-probleme-tetraedre-780363.html

Voilà le problème similaire, il me semble que il n'ya pas besoin de la partie A avant .

https://www.ilemaths.net/sujet-geometrie-vectorielle-543942.html *

Pardon mauvais lien

on était tout à fait parti sur des raisonnement sans aucune partie A de quoi que ce soit
ni aucune coordonnées de A,B,C,D etc dans un AUTRE repère (O,i,j,k) ou va savoir,
que le "repère pertinent" (A; AB; AC; AD) dans lequel les coordonnées sont comme on se tue à te dire sans aucun rapport avec d'autres dans un autre repère ni avec aucune mesure que ce soit..
et n'ont rien à voir avec ce que tu prétends.

il faut absolument que tu révises ce que veut dire des coordonnées dans un repère quelconque...

cours de seconde en géométrie plane
Repère, coordonnées, milieu, longueur d'un segment
voir encadré : "ce dont tu vas te servir dans les exercices"
......

Oui justement j'ai juste demandé si elle pouvait éventuellement servir cette partie A mais j'ai vu que il n'y en avait pas besoin... merci quand même pour l'aide

ça peut arriver à tout le monde d'avoir des difficultés en géométrie, on a sûrement pas le même âge ni la même expérience dans la matière, donc un peu de sympathie ne fait pas de mal

Merci beaucoup pour le cours @malou

d'où ma toute première intervention à 18h15, parce que par expérience, je sais que c'est souvent ce passage qui bloque
une fois cela compris, le reste se fait bien

Merci beaucoup pour votre aide