Inscription / Connexion Nouveau Sujet
Problèmes avec des fonctions...
Bonjour, j'ai beaucoup de difficultés avec cet exercice qui porte sur les fonctions. J'ai déjà répondu à quelques questions. J'ai mis les images dans un fichier Word car je ne savais pas comment faire autrement.
Enoncé et réponses:
Un paysagiste souhaite planter trois types de fleurs F1, F2 et F3 dans des carrés concentriques dont les dimensions sont données dans la figure ci-dessous. On note f1 (x), f2(x) et f3(x) les trois aires correspondantes en fonction de x.
1. L'ensemble ne doit pas dépasser 80 m de large : à quel intervalle appartient x ?
x appartient à l'intervalle ]0;55].
2. On peut montrer que, pour tout x de cet intervalle, f1(x)=x^2; f2(x)=34x+289 et f3(x)=16x+336.
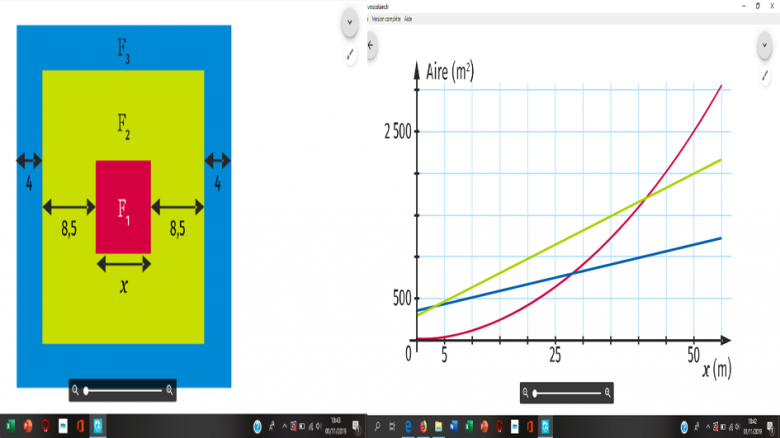
On a tracé dans un repère orthogonal les courbes représentatives des fonctions f1 ,f2,f3 sur [0;55].
a. Calculer f1(0), f2(0) et f3(0) puis identifier les courbes associées à chacune de ces fonctions.
f1(0)= 0^2=0
Donc f1 est la courbe rose car elle passe par 0.
f2(0)=34x0+289=289
Donc f2 est la courbe verte car elle est plus basse que la courbe f3.
f3(0)=16x0+336=336
Donc f3 est la courbe bleu.
b. Le paysagiste souhaite planter 1 200 m2 de fleurs F1 : déterminer graphiquement l'aire des autres fleurs.
JE NE COMPRENDS PAS CETTE QUESTION MERCI DE M'AIDER SVP
3. a. Résoudre algébriquement f2(x)=f3(x) puis interpréter.
34x+289=16x+336
34x+289-289=16x+336-289
34x-16x=16x+47-16x
18x/18=47/18
x=2,6
J'ai résous algébriquement mais je ne sais pas comment interpréter….
b. Résoudre graphiquement f1(x)=f3(x). Comment vérifier le résultat par le calcul ?
Les courbes roses(f1) et bleues(f3) se croisent au point x= environ 28m.
f1(28)= 28^2=784
f2(28)=16x28+336=784
c. Pour quelle valeur de x l'aire du terrain contenant les fleurs F1 est-elle identique à l'aire du terrain contenant les fleurs F2?
Je n'ai pas compris cette question merci de m'aider svp
Merci de votre aide
Bonjour,
x appartient à l'intervalle ]0;55]. ==> oui
f1(x)=x^2;
f2(x)=34x+289
f3(x)=16x+336.
f1(0)= 0
Donc f1 est la courbe rose ==>oui
f2(0)=289
Donc f2 est la courbe verte : oui
f3(0)=336
Donc f3 est la courbe bleue => oui
Q2b)
sur la courbe rose (f1) repère la valeur de x qui correspond à 1200 m²
qu'est ce que tu trouves ?
Merci beaucoup de ton aide . Je ne veux pas abuser de ta gentillesse mais pourrais tu m'aider avec la dernière question stp?
3a) tu ne sais pas interpréter, pourtant, il suffit de dire avec tes mots ce que tu as trouvé..
tu as trouvé que quand x environ 2,6 m, alors f2(x)=f3(x)
avec tes mots : comment peux tu "dire" que f2(x)=f3(x) ??
c. Pour quelle valeur de x l'aire du terrain contenant les fleurs F1 est-elle identique à l'aire du terrain contenant les fleurs F2?
l'aire des fleurs F1, f1(x)
l'aire des fleurs F2, f2(x)
donc la question peut s'écrire : pour quelle valeur dex a-t-on f1(x)=f2(x).
à ton avis ?
Je pensais qu'il fallait interpreter comme ceci:
f2=34x+289
=34x2,6+289=377,4
f3=16x+336
=16x2,6+366=377,6
Le problème c'est que le résultat n'est pas égal donc f2 n'égal pas f3....
tu as arrondi le résultat à 2,6 m
si tu avais gardé la fraction, ça tomberait juste.
Ton calcul est fait pour vérifier
Interpréter, c'est autre chose : c'est dire avec des mots ce qu'on avait écrit avec des termes mathématiques.
exemple
soit a : l'age de Jean
soit b : l'age de Pierre
en maths on peut écrire a=b+2
qui s'interprète "Jean a deux ans de plus que Pierre".
tu vois ?
oui, ça c'est vrai en termes mathématiques...
mais en français, tu dirais quoi ?
comme je te le disais:
tu as trouvé que quand x = environ 2,6 m, alors f2(x)=f3(x)
avec tes mots : comment peux tu "dire" que f2(x)=f3(x) ??
les deux courbes ne sont pas "égales".. deux valeurs peuvent etre égales, mais pas deux courbes.. mais tu y es presque.
La courbe verte représente f2, l'aire des fleurs de type F2,
La courbe bleue représente f3, l'aire des fleurs de type F3,
donc interpréter f2(x)=f3(x) pour x= environ 2,6 m , c'est dire
"quand x est environ = à 2.6 m, alors l'aire accordée aux fleurs de type F2 est identique à l'aire accordée aux fleurs de type F3. "
Tu comprends ?
ça c'était pour la 3a)
la 3c) à présent : A toi !
Ah d'accord merci beaucoup!!! Pour la dernière question je ne sais pas comment faire pour trouver la valeur de x et comment calculer l'aire de f2 je sais juste qu'il faut faire cxc pour un carré et lxL pour un rectangle
tu ne lis pas bien mes posts, je crois...
je t'ai dit comment faire :
c. Pour quelle valeur de x l'aire du terrain contenant les fleurs F1 est-elle identique à l'aire du terrain contenant les fleurs F2?
l'aire des fleurs F1, f1(x)
l'aire des fleurs F2, f2(x)
donc la question peut s'écrire : pour quelle valeur de x a-t-on f1(x)=f2(x).
à ton avis ?
il te suffit de résoudre f1(x)=f2(x)..
tu pourras vérifier ton résultat sur le graphique.
Désolée mais la suite de ta réponse ne s'était pas afficher…. Il faut que je résolve l'équation : x²=34x+289?
quand tu fais une lecture graphique, tu acceptes une approximation..
on dit que x est environ egal à 41, donc f1 sera environ égale à f2..
C'est normal.
Si on veut trouver la valeur exacte de x, il faudra la calculer, mais en 2nde, tu ne sais pas encore résoudre ce type d'équation..
ok ?


