Inscription / Connexion Nouveau Sujet
problèmes systèmes
encore un probleme que j ai essayé de faire dans tous les sens, mon problème c'est de formuler l'équation.
tous les éleves d'une classe étudient au moins une langue
13 étudient l'espagnol
16 étudient l'anglais
16 étudient l'allemand
4 étudient l'anglais et l'espagnol
5 étudient l'anglais et l'allemand
6 étudient l'espagnol et l'allemand
3 étudient les 3 langues
Combien y a-t-il d'élèves dans cette classe?
Merci bcp
Je te conseille de le faire en terme d'ensembles. Tu dessines trois "ronds" représentant chacun l'ensemble des élèves qui étudient l'espagnol, l'anglais ou l'allemand.
On va mettre dans chaque ensemble un nombre correspondant au nombre d'éléments (élèves) dans cet ensemble. On commencera par le bas de ta liste: dans l'intersection des trois ensembles tu mets 3 car 3 élèves étudient les 3 langues. Ensuite 6 élèves étudient l'espagnol et l'allemand, alors tu regardes l'intersection de l'ensemble "espagnol" avec l'ensemble "allemand". Il y a déjà 3 personnes et au total il y en a 6, donc on met 3 dans l'entersection des deux ensembles sans être dans le troisième...
Et ainsi de suite.
Isis
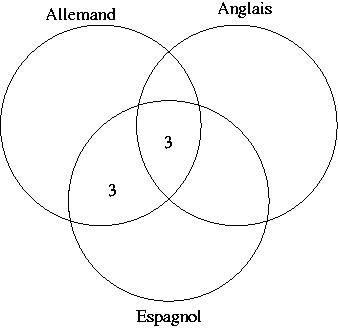
D'après ton énoncé, on trouve que 3 élèves ne font que de l'espagnol, 4 ne font que de l'anglais et 2 ne font que de l'allemand. Si tu les additionnes à ceux qui font 2 et 3 langues, tu trouves le nombre de personnes qu'il ya dans la classe, puisque toutes les catégories sont représentées: ceux qui font 1 langue, ceux qui en font 2 et ceux qui en font 3.
Cela revient aussi à additionner 13+16+16 puis à retirer 4+5+6+3
Voilà


 topologie en Bts
topologie en Bts