C'est pas clair. Si tu veux de l'aide il faut dire clairement ce qu'est g_n. Il y a ici un meli-melo avec g_n et g_n'.

cela mis à part je ne vois pas ce qu'il y a de difficile car f=1;
Donc tu utilises  la définition et cela  va te donner une intégrale de -a à a de "quelle chose" qui semble être selon ton énoncé nébuleux une fonction en escalier.
C'est tout de même pas la mer à boire. Tu devrais écrire un peu cela.

voila l'énoncer ..

** image supprimée **

bonsoir je sollicite votre aide pour un exercice que je n'arrive pas à faire ....

*** message déplacé ***

Dc

Oui ? Mais encore ?

*** message déplacé ***

dsl j'avais oublié la PJ

** image supprimée ** conformément à Sujet ancien- ne plus donner ce lien-merci

*** message déplacé ***

je nai aucune information entre a et n  afin remplacer gn' par n^2 dans l'expression

et ma fonction gn' ne depend pas de x ...

g'_n(x-s)=n^2 ssi    -1/n< x-s< 0  i.e  ssi   x<s<x+1/n  
Il faut donc considérer différent cas selon x. Il faut regarder l'intersection de
l'intervalle [x,x+1/n] et [-a,a]. ....

La charte du site exige que tu fasses l'effort de recopier tes énoncés, les scans sont interdits

*** message déplacé ***

Bonjour cela fait deux fois que tu poses la  même question. Hier soir, tard, j'ai commencé à te répondre, il faut savoir patienter de toute façon quelqu'un d'autre aurait repris le relais si je ne l'avais pas fait.  
Je continue donc ici un peu    

où     veut dire fonction indicatrice
On a encore
Il reste donc à distinguer différents cas x<a-1/n ,....   tu devras trouver une fonction affine  par morceaux et continue.




*** message déplacé ***

merciii .
Voici les différents cas trouvé . Est ce correct ?

** image supprimée ** conformément à Sujet ancien- ne plus donner ce lien-merci

moult récidive d'images non conformes
multipost....
et le règlement ......

Il faudrait donc que tu écrives ta solution, bien qu'un dessin serait plus  parlant.

que signifie mes() ?

les cas que jai pu trouvé sont:

si x a alors f*g_n'=0

SI x -a- alors  f*g_n'=0

SI  [-a,a][x,x+]
ie     x -a  et x+
ie a-x-a
alors f*g_n'=n²+1

Je ne sais pas si jai vraiment compris. Nous n'avons pas traité cela en cours donc je patoge ... je ne sais pas trop comment faire les dessins

Bonjour,  mes(A) veut dire mesure de A (mesure de Lebesgues).
Quand A est un intervalle  mes((a,b))=b-a.  
D'abord je n'ai pas l'énoncé mais je devine qu'on va faire tendre n vers l'infini.
la mesure de [-a,a] c'est  2 a   et de [x,x+1/n] c'est 1/n. Donc pour n assez grand
1/n est < 2a. Donc je pense seulement  à ce cas là.

Pour trouver le résultat il faut simplement calculer la longueur de l'intersection des 2 segments, cela dépend de x. Un petit dessin sur le papier devrait de donner les différents cas et le résultat.  

  

par exemple si x>a on n' a pas forcément f*g'_n=0.  

Non a aucun moment nous faisons tendre n vers l infini.

du coup les 2 cas où f*gn'=0 sont pour  et pour x<-a et x>a+1

est ce bien ca ?

On pose f la fonction qui vaut 1 sur l'intervalle [−a, a], a réel positif, et 0 ailleurs ; g_n' la fonction impaire qui vaut n² sur l'intervalle [−1/n, 0] et 0 en dehors de [−1/n, 1/n] ;.
1. Calculer f ∗ (g_n')
2. Montrer que g_n' est la dérivée de la fonction gn, continue, paire, qui vaut 0en
dehors de [−1/n, 1/n] et n − n²x sur[0, 1/n] ?

3. Calculer f ∗ gn et dériver cette fonction par intervalles : notée (f ∗ gn)'

4. Comparer les résultats des question 1) et 3), que peut-on écrire entre (f ∗ gn)'
et f ∗ (g_n')

Oui c'est vrai on ne fait pas tendre n vers l'infini mais l'intérêt d'un tel exercice c'est de passer à la limite. Je soupçonne (je n'ai pas vérifié)  que l'intégrale de g_n= 1  (ou bien une constante) et qu'une question intéressante à ajouter c'est que
g_n*f converge vers f (dans un certain sens).
De toute façon tu peux toujours supposer que 1/n<2a pour commencer (c'est le cas le + intéressant) et puis ensuite étudier le cas contraire.
Ici il me semble que le seul but c'est de démontrer une formule qui s'apparente à  (f*g)'=f*g'  (au moins au sens  des distributions).  

Je n'avais pas vu ta dernière solution.
C'est toute de même pas la mer à boire:
1-cas:  si x+1/n <=-a  i.e x<-a-1/n :  les deux intervalles ont une intersection vide, une mesure nulle.

2-cas   si x<a<x+1/n    l'intersection c'est :   [a,x+1/n] la mesure c'est (x+1/n-a), il faudra multiplier par n^2 que j'ai sorti de l'intervalle.  

..... et ainsi de suite....  

mercii

je ne trouve pas exactement la meme chose :

1)Si  t<-a- => f*g_n'=0

2) si -a- t<-a
=>f*g_n'= n²t+n+n²a

3)Si -at<a-
=> f*g_n'=-n²t+n-n²a

4)Si a-t<a
=> f*g_n'=-n²t-n+n²a

5) Si at<a+
f*g_n'=n²t-n-n²a

6)SI ta+
f*g_n'=0

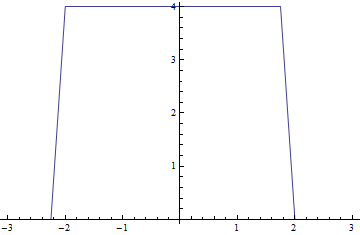
Cela ne peut pas aller. Une chose est sûre c'est que le produit va etre continue.
Donc en t=a-1/n  on doit trouver 0 (toi non) .
Ensuite quand t  >=-a  est <=a-1/n  on doit trouver une fonction constante.    

Voici la figure avec a=2 et n=1/4 ce que l'on trouve.

Est ce que tu as fait une dessin  représentant l'intervalle [-a,a] et l'intervalle [x,x+1/n]
selon les valeurs de x? Normalement il n'y a pas de difficulté à calculer la longueur de l'intersection.

non je ne vois pas comment dessiner l'intervalle . je ne sais comment dessiner [x,x+1/n]

Pouvez vous mexpliquer pour un cas etape par etape et je ferai les autre tout seul ?

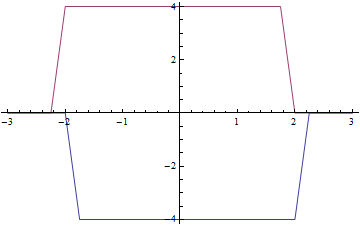
Le dessin des deux fonctions c?est bien ça ?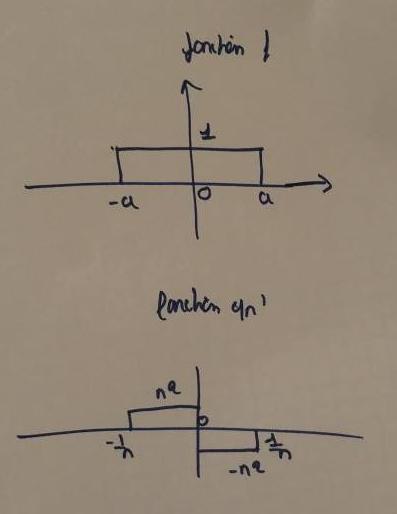



***dans le bon sens, c'est quand même mieux, non ? ...***faire ctrl+F5***

IL faut corriger. En effet l'énoncé a manque un certain  moment et j'ai travaillé avec
la fonction g'_  n^2 sur  [-1/n,0] et 0 ailleurs. Alors qu'elle vaut -n^2 sur [0,1/n].  
Donc il faut compléter:  la  fonction que j'ai considéré ce n'est pas exactement g'_n
je l'appelle h_1. on a calculé q1=  f*h_1 voir figure).
On a g'_n=h1+h_2  mais h_2(x)=-h1(-x) et comme f est paire on a
q2(x)=(f*h_2)(x)=-q_1(-x).
Voir le graphe de q1 et q2_.
Je donne la suite dans des messages différents  
ici  voir le graphe de q1 et q2

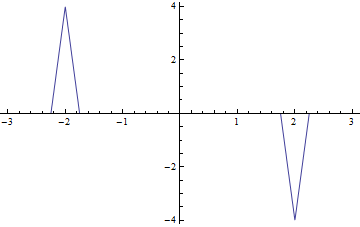
On a  donc f*g'_n=f*(h_1+h_2)=q1+q2  voir le graphe final
On voit que f*g'_n est affine par morceaux et continue.
Finalement il faut savoir  calculer q_1 que je réexplique dans le message suivant.

Je reviens donc sur le calcul de q_1=f*h_1 avec h_1= n^2 sur  [-1/n,0]  et zéros ailleurs.  
on a par définition q_1 (x)=\int_R  f1(s)q(x-s) ds
or  f1(s)q(x-s) =1*n^2 ssi s\in[a,-a] et (x-s)\in[-1/n,0] sinon zéro ailleurs
mais (x-s)\in[-1/n,0]  est équivalent à s\in [x,x+1/n]  
Je désigne I_x  l'intersection de s\in[a,-a] et de  s\in [x,x+1/n]
donc q_1(x)=n^2 \int _{I_x}  1 ds  =n^2 mes (I_x). (mes=longueur)
Il reste à calculer mes (I_x) selon les cas.
cas 1-  x<-a-1/n   i.e x+1/n <-a.  I_x est vide, sa mesure est nulle, l'intégrale est nulle.
cas 2  -a-1/n <x<-a   alors I_x=(-a-1/n,x) sa mesure est x+a+1/n et on multiplie par n^2 pour avoir l'intégrale.
cas 3 -a<x<a-1/n   donc -a<x<x+1/n<a   , I_x=[x,x+1/n]  sa mesure est 1/n, on multipie par n^2 et l'integrale =n  (c'est une constante)....
et ainsi de suite.
<

que signifie s\in[a,-a]je ne comprend pas le s\in svp ?

\in =appartient  (c'est du latex)

ah daccord je ne connais pas le language latex . apres je dois faire pareil mais avec q2 cest ca ?

est ce que je peux copié votre message qqle part pour mettre directement les symbole au lieu du language latex ayant du mal cela m'embrouille un peu

C'est parce que je n'ai pas mis les balises latex.
Le plus simple c'est d'utiliser l'editeur ici. Tu fais un copié collé
tu mets la balise LTX et tu fais aperçu

je dois mettre quel balise et où car je n'arrive pas a voir un apercu correct.
J'ai fais copié colé dans LTX en bas et apercu rien n'a changé

sans passer par q1 et q2 comment faire je ne comprend plus rien .
De base j'avais trouvé ca :

1)Si  t<-a-\frac{1}{n} => f*gn'=0

2) si -a-\frac{1}{n} t<-a . Et donc mes(-a, t+)

=>f*gn'= n2t+n+n2a

3)Si -at<a-\frac{1}{n} . Et mes(-a,t) pour -n² et mes(t,t+))
=> f*gn'=-n2t+n-n2a

4)Si a-\frac{1}{n}t<a . Et mes(t-,t) pour -n² et mes(t,a) pour n²
=> f*gn'=-n2t-n+n2a

5) Si at<a+\frac{1}{n} Et mes(t-,a)pour -n²
f*gn'=n2t-n-n2a

6)SI ta+\frac{1}{n}
f*gn'=0

Peut on reprendre depuis le début sans passer par q1 et q2 car je comprend de moins en moins

pour le cas 4 jai trouvé que la mes = n^2( a-x)
pour le cas 5 la mesure est nulle

est ce juste si oui comme ca je ferai la meme chose mais avec q2 .