Niveau LicenceMaths 2e/3e a

Produit dénombrable d'espaces complets

Posté par
Kernelpanic 23-08-19 à 11:00

Bonjour à tous,

je cherche depuis hier à démontrer qu'un produit dénombrable d'espaces complets est complet. Cela rentre dans la démonstration du théorème de Tychonov dans le cas d'une suite dénombrable d'espaces métriques compacts $(X_n, d_n)$ (on veut montrer que le produit est un espace compact et métrisable).

Dans la preuve, pour montrer tout d'abord que le produit X est métrisable, on définit la distance

$d(x,y) = \sum_{1}^{\infty} 2 ^{-n}d_n(x_n,y_n) \text{ si } x=(x_n), y=(y_n) \in X$

on démontre que d est bien une distance et que l'application

$id : (X, \mathcal{T}) \to (X,d)$ est bicontinue.

Maintenant pour prouver que l'espace est compact, le livre veut montrer qu'il est complet et précompact (je sais qu'on peut le prouver plus rapidement en prouvant que toute suite admet une sous-suite convergente, mais je trouve plus intéressant de prouver les deux derniers points énoncés précemment).

Néanmoins, le livre montre juste que (X,d) est précompact et nous dit juste que pour prouver la complétude, il faut travailler coordonnées par coordonnées.

J'ai prouvé, en utilisant le fait que chaque (Xn, dn) est compact et donc complet (+ précompact mais on s'en fiche ici), que pour une suite de Cauchy dans X $x_n = (x_n^i)$ (en indexant i pour l'espace Xi), chaque suite $x_n^i$ était une suite de Cauchy et donc converge vers $a_i \in X_i$ .

Mais j'ai du mal à démontrer que $x_n \to a = (a_i)$ , je ne sais pas trop comment m'y prendre. J'ai toujours un peu de mal avec cette notion d'infini. J'ai pensé à prendre une boule centrée en a et de rayon 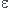, dire qu'elle contient

un ouvert élémentaire $\prod_{i \in I fini} \omega_i \times \prod_{j \notin I} X_j$ contenant a et bidouiller un peu pour obtenir une inégalité en 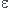mais ça mène pas à grand chose...

Merci d'avance pour vos réponses.

Posté par re : Produit dénombrable d'espaces complets 23-08-19 à 11:08

J'ai oublié quelque chose pour ceux qui se demandent !

Dans l'énoncé, et pour la distance d, on suppose que $\forall n \in \N, d_n \leq 1$

quitte à remplacer $d_n$ par la métrique équivalente $\dfrac{d_n}{1+d_n}$

Posté par re : Produit dénombrable d'espaces complets 23-08-19 à 11:33

Bonjour Kernelpanic.

Je reprends tes notations. Effectivement il reste à démontrer que $d(x_n,a)\underset{n\to+\infty}{\to}0$ .

$d(x_n,a)=\sum_{i=1}^{+\infty}\frac{d_i(x^i_n,a_i)}{2^i}$ .

Soit $\varepsilon>0$ . Pour tout $N\in\N^*$ , on a
$d(x_n,a)=\sum_{i=1}^N\frac{d_i(x^i_n,a_i)}{2^i}+\sum_{i=N+1}^{+\infty}\frac{d_i(x^i_n,a_i)}{2^i}\le\sum_{i=1}^N\frac{d_i(x^i_n,a_i)}{2^i}+\sum_{i=N+1}^{+\infty}\frac{1}{2^i}$ ,
où on utilise le fait que $d_i\le 1$ .

Puisque l'on a la liberté du choix de $N\in\N^*$ , fixons-en un tel que $\sum_{i=N+1}^{+\infty}\frac{1}{2^i}<\varepsilon$ . On a donc
$d(x_n,a)\le\sum_{i=1}^N\frac{d_i(x^i_n,a_i)}{2^i}+\varepsilon$ .

Ensuite, puisque l'on a affaire à une somme finie, on peut affirmer qu'à partir d'un certain rang $n$ assez grand, $\sum_{i=1}^N\frac{d_i(x^i_n,a_i)}{2^i}<\varepsilon$ . On a donc montré qu'à partir d'un certain rang, $d(x_n,a)<2\varepsilon$ . Donc $d(x_n,a)\underset{n\to+\infty}{\to}0$ .

Posté par re : Produit dénombrable d'espaces complets 23-08-19 à 11:38

Bonjour WilliamM007, comme d'habitude : toujours au rendez-vous

C'est encore plus simple que ce je venais de trouver avec les ouverts élémentaires ! (l'idée était la même mais je m'embrouillais avec une multitude d'indices inutiles...).

Un grand merci (comme toujours), passe une bonne journée

Posté par re : Produit dénombrable d'espaces complets 23-08-19 à 11:42

Je t'en prie, bonne journée à toi aussi

Ce topic

Imprimer
Réduire / Agrandir
Pour plus d'options, connectez vous !
Fiches de maths

topologie en post-bac
7 fiches de mathématiques sur "topologie" en post-bac disponibles.

Rechercher

Espace membre

Zone membre

Pas de compte ?
Je m'inscris

Changer d'île

Cours et Exercices de maths

Forum de maths

college

lycee

Outils de maths

Pages les plus populaires

Produit dénombrable d'espaces complets

Seuls les membres peuvent poster sur le forum !

Ce topic

Fiches de maths