Bonjour,
Vérifie
B(-1;10)

2)
équation du plan BCD

b) -2x+3y+z+d=0
que vaut d?

Re,
1) j'ai oublié de mettre l'aire du triangle rectangle BCD soit (5 * 70)/2=(514)/2

2b) oui je venais de voir
-2x+3y+z+d=0
soit (-2*-1)+3*1+1*0+d=0
6+d=0  donc d= -6
ce qui donne
-2x+3y+z-6=0
3)la droite d passe par A
x=5-2t
y=-5+3t   t
z=2+t
4) -2x+3y+z-6=0
-2(5-2t)+3(-5+3t)+(2+t)-6=0
-10+4t-15+9t+2+t-6=0
14t-29=0  t=29/14
xh=5-2(29/14)=6/7
yb=-5+3(29/14)=17/14
yh=2+1(29/14)= 57/14


MERCI

tu peux vérifier  D(6;-6;-1)

Re,

comment faire pour vérifier comme tu dis

MERCI
je vais poursuivre après

Re,
en recopiant au propre j'ai fait une erreur donc je rectifie
1) produit scalaireBC.CD=0 donc BCD est rectangle en C de plan BCD
BC=racine de 5
CD= racine de 70 donc différent le triangle n'et pas isocèle en C
l'aire du triangle rectangle BCD soit (5 * 70)/2=(514)/2
2a) BC.n =0
CD.n=0
donc le vecteur  est un vecteur normal du plan (BCD)
b)-2x+3y+z+d=0
soit (-2*-1)+3*1+1*0+d=0
5+d=0  donc d= -5
ce qui donne
-2x+3y+z-5=0
3)x=5-2t
y=-5+3t   t
z=2+t
4) -2x+3y+z-5=0
-2(5-2t)+3(-5+3t)+(2+t)-5=0
-10+4t-15+9t+2+t-5=0
14t-28=0  t=28/14=2
xh=5-2(2)=1
yb=-5+3(2)=1
yh=2+1(2)= 4

PLSVU : comment faire pour vérifier :"tu peux vérifier  D(6;-6;-1)"

J'attend votre réponse avant de continuer

MERCI

C(0;1;2) et D(6;-6;-1)



tu trouves
CD= racine de 70
CD.n=0

autre erreur de frappe
Sans un repère orthonormé de l'espace

dans ce cas on ne peut pas détermlner  par calcul , les longueurs des segments

Re,
je ne comprend pas ce que tu veux dire.
est-ce que ce que j'avais fait était bon

5) déterminer le volume du tétraèdre ABCD
V=1/3*aire*ht
je prend quoi comme hauteur ? (j'ai pensé car j'ai fait un petit dessin à CD°

MERCI

Re,

j'ai C(0;1;2)   D(6;6;-1)
vecteur CD (6-0=0;6-1=5;-1-2=-3)

je ne trouve pas comment toi

MERCI

evidemment
puisque tu a s tapé ceci:
Sans un repère orthonormé de l'espace, on considère les points A(5;-5;2) B(-1;10) C(0;1;2) et D(6;-6;-1)
et je t'ai demande de verifié.....

je t'ai demandé de vérifiER....

Re,
en effet grosse erreur de frappe enfin j'ai oublié de mettre le ; il faut donc lire :
Dans un repère orthonormé de l'espace, on considère les points A(5;-5;2) B(-1;1;0) C(0;1;2) et D(6;-6;-1)

ok

merci de vérifier ce que j'avais fait

et merci de me dire comment je peux faire pour trouver le volume . Quel est la hauteur ?

MERCI (et encore excuses moi pour les erreurs de frappe)

tu persistes pour les coordonnées du point D

Re,
Encore une erreur de ma part D(6;6;-1)
pour le 5
comment savoir que je dois prendre la hauteur issue de A ?
je prend quoi A... (pour moi AB=AC=AD non ?°

MERCI

  la hauteur issue de A doit être...................

Re,

j'avoue que je suis perdue
je n'arrive même pas à faire ce dessin, c'est vraiment la galère. Je sais faire des choses mais le problème c'est que je ne sais quand le faire, j'ai du mal à comprendre quand je dois calculer ça ou ça. Enfin....
là pour la hauteur peut-être avec le H que l'on a calculer au-dessus
donc AH = 214
Volume = 1/3*(514/2)*214=46,67

6a) calculer les longueurs AB et AC
AB =76
AB=61   AB.AC=66
angle BAC= cos(angle BAC)+ 66/576*61
puis cos^-1= 14,23°

MERCI

  Dans un triangle chaque  hauteur  , issue d'un sommet est perpendiculaire au coté opposé au sommet
Dans  un tétraèdre  chaque hauteur  issue d'un sommet est perpendiculaire ...........

Re,
Dans un triangle chaque  hauteur  , issue d'un sommet est perpendiculaire au coté opposé au sommet
Dans  un tétraèdre  chaque hauteur  issue d'un sommet est perpendiculaire au côté opposé au sommet
donc ici à DB donc  longueur de BD= 53
Volume = 1/3*(514/2)*53=12,98

MERCI

Dans  un tétraèdre  chaque hauteur  issue d'un sommet est perpendiculaire au côté opposé au sommet NON

tape  dans  ton moteur de recherche  "hauteur dans un tétraèdre" et observe les images

image

Re,
je suis désolée mais je galère avec l'espace.
J'ai fait dans le recherche mais je n'y comprend rien
c'est-à-dire je n'arrive déjà pas à faire le croquis de mon exercice donc c'est dur sans schéma
donc si je comprend ils faut faire les médianes des hauteurs ABC
l'intersection de ses 3 médianes forment le pied de la hauteur issue de A c'est ça

ce n'est pas AH ?  

je suis perdue

MERCI

La hauteur issue du sommet A  est perpendiculaire à la face  BCD   tu indiques clairement donc c'est  ..............
( tu affirmes , sans point d'interrogation)

Re,
donc on est d'accord tu as tracé les 3 médianes. et l'intersection des 3 te donne H
c'est bizarre mais ça ne semble pas être le milieu  par exemple de BB'

je ne sais plus la médiane c'est bien le milieu
ou alors doit-on tracer pour que la droite soit perpendiculaire du sommet

MERCI (j'ai beaucoup de lacunes, excusez moi si ça vous semble bête)

MERCI

Re,
et comment calculer AH ?   d'après ce que j'ai calculé j'ai 36

MERCI

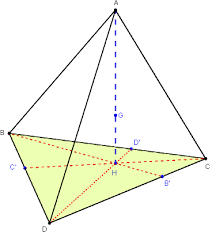
    l'image est un tétraèdre de base  BCD  , ( triangle quelconque )  de base A
_{dans le triangle BCD  sont tracées les hauteurs  de  triangle (  on n'est pas obligé de les  tracer)  ,}
la droite (AH)  est la perpendiculaire issue  de A perpendiculaire, elle coupe la base BCD en H
le segment [AH]    est la hauteur  issue de A  du tétraèdre ABCD  .

Re,
donc c'est bon pour la dimension AH : 36

MERCI

d'après ce que j'ai calculé j'ai   AH= 3√6

indique ton calcul  c'est faux

image  du tétraèdre  , obtenu avec les données  correctes de l 'énoncé

Re,
merci pour ce schéma, j'aimerai tellement savoir le faire, j'ai essayé sur géogébra mais pas moyen.
Vecteur AH (-4;6;2)   A(5;-5;2)     H(1;1;4)
longueur AH  : -4²+6²+2²=56=214 (j'avais fait une erreur en recopiant
Volume = 1/3*(514)/2*214=23,33

et pour le 6 c'est bon ?

AVEC votre croquis je vois mieux.
MERCI

  attention tu as oublié les parenthèses
longueur AH  : (-4)²+6²+2²=56=214
AH=2√14
    tu calcules le volume du tétraèdre
  

  tu donnes en  la valeur exacte
Volume =   1/3*(5(14)/2)*214=23,33

Re,
Oui mais la réponse est bonne (-4)*(-4)=16
volume : 1/3*(514)/2)*214=70/3

et merci de me dire quoi pour la question 6 a et 6 b

MERCI

Re,
Merci de me dire quoi pour clôturer cet exercice

MERCI

Oui mais la réponse est bonne (-4)*(-4)=16 à condition de mettre des parenthèses
sinon -4²=-16
ensuite de mettre aussi celles-ci √(........)
longueur AH  : ((-4)²+6²+2²)=√56=2√14
OK pour le volume70/3
AB=√76  OK
AC=√61  OK
AB*AC=√(76*61)≠66???
angle BAC= cos(angle BAC)+ 66/5√76*√61?????
cette égalité n'a aucun sens
_{un angle s'exprime en degré ou  en radian, un cosinus est un nombre sans unité de grandeur, et  √76√61    est une aire     exprimée  en unité de longueur au carré}  

formule du théorème à  appliquer

_{de part et d'autre du signe d'égalité    la grandeur  s'exprime en    en unité de longueur au carré}

Re,
encore une fois perdue
je vais reprendre
donc :
moi j'ai d'après mes exercices résolus
BAC=cos(BAC) (vecteursAB.AC)/(AB*AC)
donc vecgteursAB.AC j'ai 66
donc 66/(√76*√61) ce qui me donne en degré 14,23 °

MERCI

    rédaction à revoir
BAC=cos(BAC) (vecteursAB.AC)/(AB*AC)

tu dois partir  de cette égalité pour déterminer   la valeur  de


Ecris les toutes  étapes du calcul en gardant les termes exprimés avec les lettres

Comme  tu n'utilises pas le théorème d'Al-Kashi,   je te rappelle  certaines notations  afin que tu corriges  ta rédaction
Dans un triangle ABC rectangle en A:

Produit scalaire
1)Norme d'un vecteur .

la norme du vecteur, est la distance AB

2)Produit scalaire dans l'espace
Soient   et    deux vecteurs  de l'espace et trois points A,B et C  tels que
  et  
Le produit scalaire  de par noté  , ,est le nombre réel définit  par




3) Produit scalaire dans un repère orthonormé

Soient  et   deux vecteurs  de coordonnées respectives (x,y,z)  et (x',y',z')




pour rédiger correctement  relis ce lien
Un cours complet sur le produit scalaire

Bonjour,
@PLSVU,
Je ne crois pas que ça intervienne dans l'exercice, mais j'ai un gros doute sur ceci :

Bonjour,
je reprend donc cet exercice
donc les vecteurs AB produit scalaireAC  donc AB.AC= longueurs AB * longueur AC * cos de l'angle BAC

dans un exercice de mon livre pour calculer l'angle BLC
on calcule le produit scalaire des vecteurs LB.LC = longueurs LB* Long LC* cos angle BLC donc cos angle BLC= numérateur le produit scalaire LB.LC et au dénominateur le produit LB*LC

c'est pourquoi je suis perdue

MERCI

Bonjour Sylvieg

L'image est un tétraèdre de base  BCD  , ( triangle quelconque )  de sommet  A..
_{je corrige}

L'image est mal choisie ,   car la hauteur, du  tétraèdre ABCD ,  issue de A  coupe  la base   BCD en H , orthocentre de la base.,ce qui n'est pas toujours le cas  
_{pour Nelcar  intersection des  médianes}
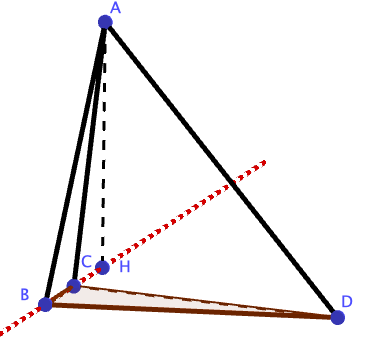
J'ai  pris le temps de faire la figure  correspondant à l'exercice , où on peut voir que la hauteur issue de A , ne coupe pas la base BCD,  le point H , intersection de d et (BCD) est le projeté de A sur le plan (BCD)

les questions 3) déterminer une représentation paramétrique de la droite d orthogonale au plan (BCD) et passant par le point A
et 4) Déterminer les coordonnées du point H, intersection de la droite d et du plan(BCD)  permettent  de calculer la mesure  de la  hauteur  .( la démarche est donnée)


_{pour la  dernière question . j'espère que  Nelcar va écrire des égalités correctes.pour  déterminer la valeur de l'angle BAC}

Nelcar
je viens de voir ton message

re,

je viens de regardé le théorème d'al-Kashi, si quelqu'un peut me mettre avec ce théroème ce qu'il aurait fallu que je fasse

je reviens donc on a :
AB.AC= longueurs AB * longueur AC * cos de l'angle BAC
76*61*cos angle BAC
cos angle BAC = 76/61=1,116199641

je ne sais plus je suis encore une fois perdue

MERCI

Re,
je viens d'essayer avec le théorème d'Al-kashi
j'ai fait
5=76+61-2*76*61cos A
cos a=132/136,18=0,969
cos^-1 = 14,23°

MERCI de me dire quoi

Re,
et de cette façon je retrouve la façon de ma livre
d'après mes exercices résolus
BAC=cos(BAC) (vecteursAB.AC)/(AB*AC)
donc vecgteursAB.AC j'ai 66
donc 66/(√76*√61) ce qui me donne en degré 14,23 °

MERCI Pour votre réponse

BAC=cos(BAC) (vecteursAB.AC)/(AB*AC)