Inscription / Connexion Nouveau Sujet
produits de matrices 3*2 et 2*3
Bonjour,
voici l'exercice sur lequel je bloque :
A est une matrice 3*2
B est une matrice 2*3
on sait que (AB)2 = AB , montrer que BA = I2
(AB)2 = AB donc AB*AB = AB ou encore A*(BA)*B = AB
on "voit" bien que BA=I2 est une condition suffisante mais pourquoi est-elle nécessaire ?
merci pour votre aide
salut
on peut :
écrire A =
a b
c d
e f
et B =
g h i
j k l
et résoudre le système (AB)2 = AB
on peut considérer les morphismes associés aux matrice A et B et raisonner en considérant noyau et image sachant que AB = p est un projecteur ...
Bonjour,
c'est faux. As-tu recopié correctement ton exercice ?
N'as-tu pas de conditions d'inversibilité pour AB ?
merci beaucoup pour vos interventions
effectivement, j'ai mal lu l'énoncé : A et B sont deux matrices de rangs 2, je vais donc revoir les propriétés du rang sur la multiplication des matrices
je donne un coup de main à un élève de Maths Sup et je n'ai aucune connaissance sur les "projecteurs" : je vais essayer de travailler cette partie du cours
je ne trouve pas en quoi le rang des matrices A et B va m'aider à trouver la réponse à la question....
suis bloquée... 
Bonjour garnouille
Le rang de est égal à celui de
. En déduire pourquoi l'écriture
a un sens et en tirer toutes les conséquences sur l'écriture de GBZM.
Idem pour .
Ce n'est pas du tout ce vers quoi j'essayais d'aiguiller !
Simplement, si sont trois application linéaires telles que
, que
est injective et
surjective, que peut-on dire de
?
merci à tous les intervenants !
tA*A étant une matrice 2*2 de rang 2, elle est inversible et son inverse est une matrice 2*2
de plus tA est une matrice 2*3 donc le produit (tA*A)-1 tA existe, on peut donc multiplier à gauche chaque membre de l'égalité obtenue par GBZM :
A*(BA - I2)*B = 02
( tA*A)-1 tAA*(BA - I2)*B = (tA*A)-1 tA*02 = 02
(BA - I2)*B = 02
avec un raisonnement analogue sur B, on obtient
BA - I2 = 02 d'où BA = I2
est-ce correct ?
Ce n'est pas du tout ce vers quoi j'essayais d'aiguiller !
Oui, mais ça donne explicitement un inverse, même si ce n'est pas demandé. Je trouve que c'est intéressant
je ne maîtrise pas le cours, il faut que je revois les liens entre le rang et l'injectivité et/ou la surjectivité...
encore merci à TOUS
garnouille, tu peux aussi montrer qu'une application linéaire injective(resp. surjective) est inversible à gauche(resp. à droite).
je ne maîtrise pas le cours, il faut que je revois les liens entre le rang et l'injectivité et/ou la surjectivité...
encore merci à TOUS
Ce n'est pas très compliqué. Une application linéaire (dimension p vers n) est surjective si son rang est égal à n. Si une application linéaire est surjective, alors sa transposée est injective.
il faut que je revois les liens entre le rang et l'injectivité et/ou la surjectivité...
Oui, ça me semble indispensable de comprendre ça. Ce n'est pas dur : une application linéaire est injective si et seulement si son noyau est nul, c.-à-d. si et seulement si son rang est égal à la dimension de l'espace de départ ; une application linéaire est surjective si et seulement si son image est l'espace d'arrivée, c.-à-d. si et seulement si son rang est égal à la dimension de l'espace d'arrivée. (Ici tous les espaces sont de dimension finie).
À titre très personnel, j'ai apprécié toutes vos interventions, elles se complètent sont faites dans le respect des autres … ça m'a permis d'avancer malgré 11h de décalage horaire !…
Cette fois, je vais (tenter de) retenir le lien entre rang et injection/surjection !
de rien ...
je t'ai proposé une réponse très naïve (et fastidieuse !!) valable en petite dimension !!!
parler de projecteur était juste là pour voir avec l'idée de noyau et d'image donc de rang ... mais si tu ne connais pas ...
je voulais en fait te proposer ensuite ce que GBZM a donné et qui m'a devancé ...
Une petite mise en garde : rien dans l'énoncé n'indique sur quel corps on travaille. Supposons qu'on travaille sur , le corps à deux éléments, et soit
. Alors
est de rang 2, mais le produit
n'est pas inversible !
La voie que j'ai suggérée n'a pas besoin d'hypothèse sur le corps.
Génial GBZM! Effectivement pour , j'avais supposé
comme corps de base. Et en plus, si on veut proposer à garnouille cette méthode, il faudrait faire démontrer cette propriété…J'avais aussi pensé à un contre-exemple dans
(genre
avec des
et des 1, pour avoir un rang nul à la fin par exemple…
Bref, rien à dire, les pistes de carpediem et GBZM sont clairement meilleures…
encore une question et d'avance merci
je crois que je me suis pris les pieds dans le tapis avec les dimensions....:
Soit u l'application linéaire associée à A matrice 3*2
u est une application de 
2 dans 3
comme rg(A) = 2 (= n) , u est injective et donc
"si A*M = 03 alors M= 03 "
comment justifie-t-on la propriété entre les guillemets ?
je n'ai rien trouvé dans le cours
Bonsoir garnouille
Si je peux me permettre, injective te donne l'existence d'un inverse à gauche. Il s'agit même d'une équivalence(très bon exercice, car tu verras comme GBZM l'a précisé, qu'on n'a pas besoin de travailler sur un corps particulier).
Je te dis cela car ton exercice ne demande pas d'avoir un inverse explicite, donc on s'en fiche. Je t'ai donné une méthode donnant un inverse explicite, MAIS :
- il te faut démontrer une propriété pas évidente pour ton élève à mon avis
- ce n'est valable que sur …
Donc, tu vois….
Tout simplement en utilisant le fait que "injectif" pour une application linéaire veut dire "de noyau nul". autrement dit entraîne
. Il me semble que ça, c'est dans tous les bons cours.
Il reste un tout petit peu de travail pour en déduire "Si , alors
"
o en utilisant le fait que "injectif" pour une application linéaire veut dire "de noyau nul". autrement dit A*x=0 entraîne x=0. Il me semble que ça, c'est dans tous les bons cours.
oui, oui, ça je comprends bien pour "x" vecteur colonne 3*1 ici mais pour une matrice M de taille 3*3 ?
Que dire de l'image de M si AM=03?
en fait, je ne sais plus trop "qui est qui" !
A est une matrice 3*2 danc l'application est de
2 dans 3
M n'est pas un vecteur de
2 mais une matrice 3*3, du coup, je ne vois pas comment faire le lien entre M et l'application représentée par ABonjour
Je ne vois pas ce qui te pose problème.
Si est la matrice nulle de dimension 2, alors pour tout vecteur
à 2 lignes et 1 colonne,
est le vecteur nul à 2 lignes et 1 colonne.
Annuler
connectez vous
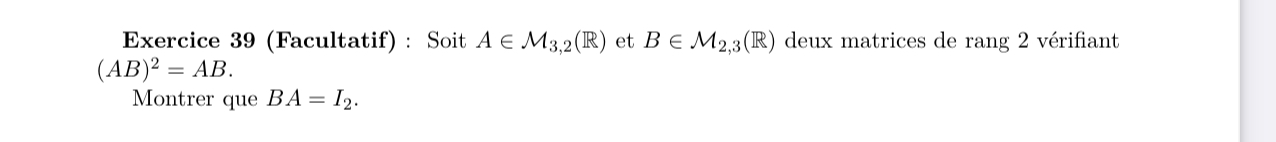
algèbre en post-bac